Ctrl+K

Hybrid Discontinuous Galerkin methods

4.4. Hybrid Discontinuous Galerkin methods#

use additionally the hybrid facet variable on the skeleton:

\[ A(u,\widehat u; v, \widehat v) = \sum_T \int_T \nabla u \nabla v - \sum_T \int_{\partial T} n \nabla u (v-\widehat v) - \sum_T \int_{\partial T} n \nabla v (u-\widehat u) + \frac{\alpha p^2}{h} \sum_F \int_F (u-\widehat u)(v-\widehat v) \]

the jump-term is now replaced by the difference \(u - \widehat u\).

No additional matrix entries across elements are produced. Dirichlet boundary conditions are set as usual to the facet variable:

from ngsolve import *
from ngsolve.webgui import Draw
from netgen.occ import *

def AtomicShape(maxh = 0.1):
    ax2d = gp_Ax2d(gp_Pnt2d(0.5, 0.5), gp_Dir2d(1, 0))
    outeli = Ellipse( ax2d, 0.5, 0.1)
    ineli = Ellipse( ax2d, 0.3, 0.06)

    shape = outeli.Face() - ineli.Face() 


    shape += shape.Rotate(gp_Ax1(gp_Pnt(0.5, 0.5, 0), gp_Dir(0,0,1)), 120)
    shape += shape.Rotate(gp_Ax1(gp_Pnt(0.5, 0.5, 0), gp_Dir(0,0,1)), 240)
    shape += Circle((0.5,0.5),0.2).Face() 

    Draw(shape)
    geo = OCCGeometry(shape, dim = 2)
    return Mesh(geo.GenerateMesh(maxh = maxh)).Curve(3)

mesh = AtomicShape()

order=2
V = L2(mesh, order=order)
F = FacetFESpace(mesh, order=order, dirichlet=".*")
fes = V*F
u,uhat = fes.TrialFunction()
v,vhat = fes.TestFunction()

Now, the jump is the difference between element-term and facet-term:

jump_u = u-uhat
jump_v = v-vhat

r_centr = (x-0.5)**2+(y-0.5)**2

f = LinearForm(100*exp(10*r_centr)*v*dx).Assemble()

alpha = 4
condense = False
h = specialcf.mesh_size
n = specialcf.normal(mesh.dim)

a = BilinearForm(fes, condense=condense)
dS = dx(element_boundary=True)
a += grad(u)*grad(v)*dx + \
    alpha*order**2/h*jump_u*jump_v*dS + \
    (-grad(u)*n*jump_v - grad(v)*n*jump_u)*dS

b = CF( (20,1) )
uup = IfPos(b*n, u, uhat)
a += -b * u * grad(v)*dx + b*n*uup*jump_v *dS
a.Assemble()

#f = LinearForm(1*v*dx).Assemble()

gfu = GridFunction(fes)

print ("A non-zero elements:", a.mat.nze)

A non-zero elements: 181395

if not condense:
    inv = a.mat.Inverse(fes.FreeDofs(), "pardiso")
    gfu.vec.data = inv * f.vec
else:
    fmod = (f.vec + a.harmonic_extension_trans * f.vec).Evaluate()
    
    inv = a.mat.Inverse(fes.FreeDofs(True), "pardiso")
    gfu.vec.data = inv * fmod
    
    gfu.vec.data += a.harmonic_extension * gfu.vec
    gfu.vec.data += a.inner_solve * f.vec

Draw (gfu.components[0], mesh, "u-HDG");

4.4.1. Remarks on sparsity pattern in NGSolve#

import scipy.sparse as sp
import matplotlib.pylab as plt
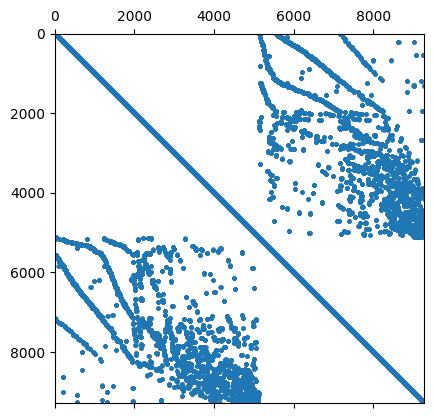
A = sp.csr_matrix(a.mat.CSR())
plt.spy(A, markersize=2)

<matplotlib.lines.Line2D at 0x7fbfbf8e4ed0>
../_images/dc32e2b1e71fb44e9e2dfd8e6d5ee5f49963dff38793ea01c4015c7e5167e7d0.png

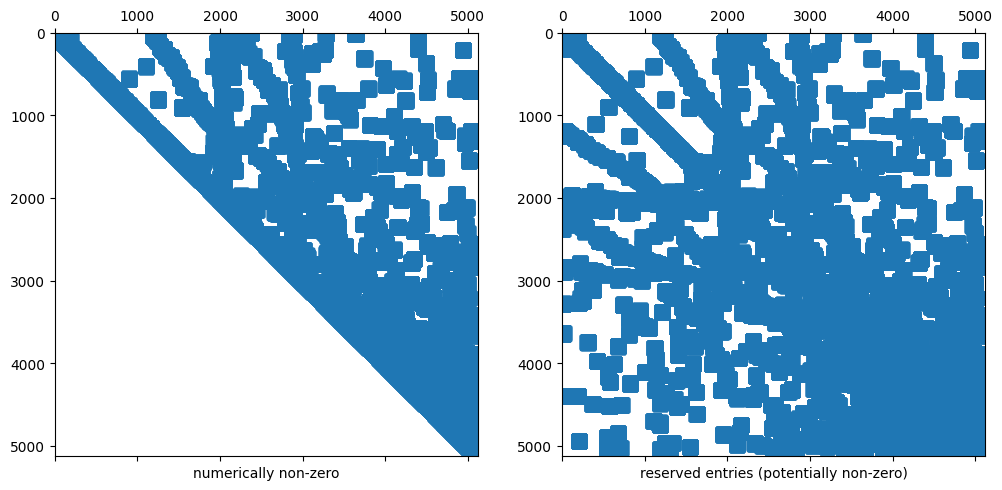
4.4.1.1. Remark 1: The sparsity pattern is set up a-priorily#

  • The sparsity pattern of a sparse matrix in NGSolve is independent of its entries (it’s set up a-priorily).

  • We can have “nonzero” entries that have the value 0

Below we show the reserved memory for the sparse matrix and the (numerically) non-zero entries in this sparse matrix.

fes2 = L2(mesh, order=order, dgjumps=True)
u,v=fes2.TnT()
a3 = BilinearForm(fes2)
a3 += u*v*dx + (u+u.Other())*v*dx(skeleton=True)
a3.Assemble();

import scipy.sparse as sp
import matplotlib.pylab as plt
plt.rcParams['figure.figsize'] = (12, 12)
A = sp.csr_matrix(a3.mat.CSR())
fig = plt.figure(); ax1 = fig.add_subplot(121); ax2 = fig.add_subplot(122)
ax1.set_xlabel("numerically non-zero"); ax1.spy(A)
ax2.set_xlabel("reserved entries (potentially non-zero)"); ax2.spy(A,precision=-1)
plt.show()
../_images/33b9146d17a6340969715d0c276e0c211c8636b0ae86460c1cfb3f6507d2fe6e.png

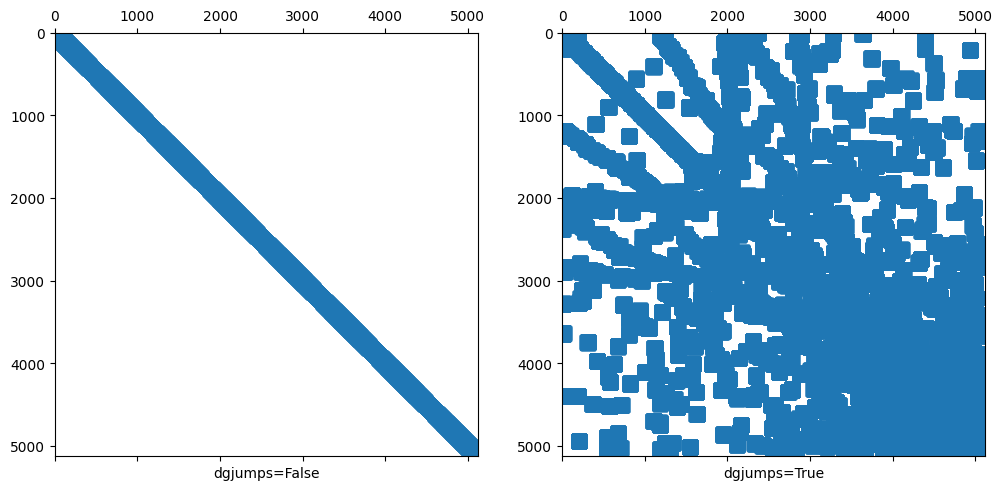
4.4.1.2. Remark 2: Sparsity pattern with and without dgjumps=True is different#

a1 = BilinearForm(L2(mesh, order=order, dgjumps=False)); a1.Assemble()
a2 = BilinearForm(L2(mesh, order=order, dgjumps=True)); a2.Assemble()
A1 = sp.csr_matrix(a1.mat.CSR())
A2 = sp.csr_matrix(a2.mat.CSR())
fig = plt.figure(); ax1 = fig.add_subplot(121); ax2 = fig.add_subplot(122)
ax1.set_xlabel("dgjumps=False"); ax1.spy(A1,precision=-1)
ax2.set_xlabel("dgjumps=True"); ax2.spy(A2,precision=-1)
plt.show()

used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )
../_images/8feba7b6acdc5fba102640128f41d2426deb406db69cb21c6002145c0903c0ed.png

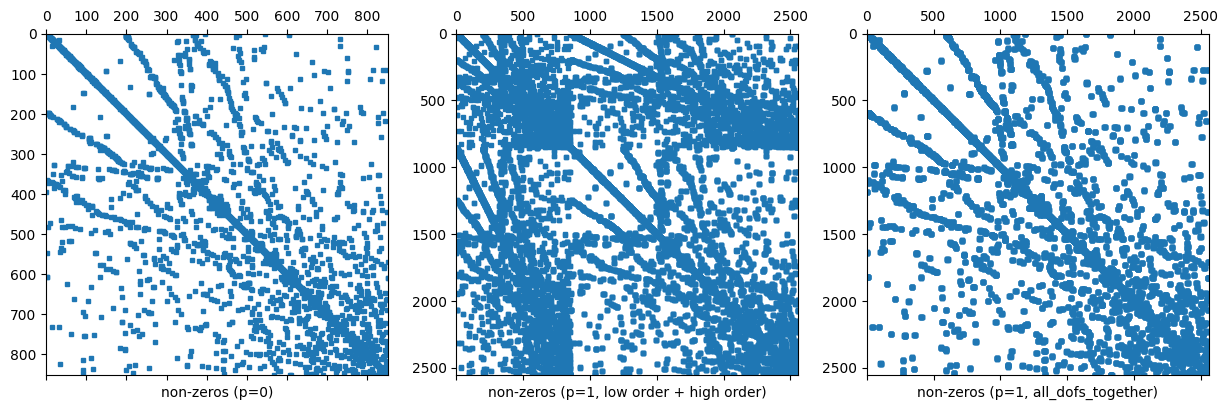
4.4.1.3. Remark 3: Dof numbering of higher order FESpaces#

  • In NGSolve FESpaces typically have a numbering where the first block of dofs corresponds to a low order subspace (which is convenient for iterative solvers).

  • For L2 this means that the first dofs correspond to the constants on elements.

  • You can turn this behavior off for some spaces, e.g. for L2 by adding the flag all_dofs_together.

We demonstrate this in the next comparison:

plt.rcParams['figure.figsize'] = (15, 15)
fig = plt.figure()
ax = [fig.add_subplot(131), fig.add_subplot(132), fig.add_subplot(133)]

for i, (order, all_dofs_together, label) in enumerate([(0,False, "non-zeros (p=0)"),
                                                    (1,False,"non-zeros (p=1, low order + high order)"),
                                                    (1,True,"non-zeros (p=1, all_dofs_together)")]):
    a = BilinearForm(L2(mesh,order=order,dgjumps=True,all_dofs_together=all_dofs_together))
    a.Assemble()
    ax[i].spy(sp.csr_matrix(a.mat.CSR()),markersize=3,precision=-1)
    ax[i].set_xlabel(label)
../_images/5cbf435ee4ba1504a155467bb9e7a21dcc9120bb7475c9a9ff38407d1e186580.png
Contents