11.4. HDG Tricks (scalar)#
In this unit we want to discuss a few advanced tricks that can be used for further tuning of the \(H(\operatorname{div})\)-conforming Hybrid DG Stokes discretizations (and other 2nd order elliptic problems).
We want to treat:
projected jumps
🫣
hiddendofsHybrid DG formulations based on lifting operators
For ease of discussion we will first start with a discussion of the first three features in the context of the Poisson problem
and will apply it directly afterwards to the Stokes problem.
Note
We will partially repeat the introduction of the projected jumps approach from the advanced tutorials here in order to provide a self-contained discussion and keep a consistent notation. Furthermore we will give more details on the tricks behind the curtain.
11.4.1. Preliminary: Recap of standard HDG #
The standard interior penalty DG method for the Poisson problem takes the form:
\(V_{h,g} = V_h^T \times \hat V_{h,g}\)
\(V_h^T = \mathbb{P}^{k}(\mathcal{T}_h)\) (discontinuous pol. on elements)
\(\hat V_h = \mathbb{P}^{k}(\mathcal{F}_h)\) (discontinuous pol. on facets), \(\hat V_{h,g} = \{\hat v \in \hat V_{h} \mid \hat v = \Pi^k g \text{ on } \partial \Omega\}\)
\(\underline{u}_h = (u_h,\hat u_h) \in V_{h,g}\) solves \(a_h(\underline{u}_h, \underline{v}_h) = f_h(\underline{v}_h)\) for all \(\underline{v}_{h} \in V_{h,0}\) with
HDG bilinear form \(a_h(\cdot,\cdot)\): \(\newline\displaystyle a_h(\underline{u}_h,\underline{v}_h) := \underbrace{\sum_{T \in \mathcal{T}_h} \int_T \nabla u \cdot \nabla v}_{=:b_h(u_h,v_h)} \underbrace{- \int_{\partial T} \nabla u \!\cdot \! n \cdot (v - \hat v)}_{=: N_h({u}_h,\underline{v}_h)} \underbrace{- \int_{\partial T} \nabla v \! \cdot \! n \cdot (u - \hat u)}_{= N_h({v}_h,\underline{u}_h)}\) \(\newline\displaystyle \hphantom{a_h(\underline{u}_h,\underline{v}_h) := }\underbrace{+ \frac{\gamma k^2}{h}\int_{\partial T} (u - \hat u) \cdot (v - \hat v)}_{=: S_h(\underline{u}_h,\underline{v}_h)},\)
HDG linear form \(f_h(\underline{v}_h)\): \( \newline\displaystyle f_h(\underline{v}_h) := \sum_{T \in \mathcal{T}_h} \int_T f v\).
Show code cell source
# input : fes = V x Vhat:
def setup_HDG_system(fes, **opts):
uh, vh = fes.TnT()
(u,uhat), (v,vhat) = uh, vh
jump = lambda uh: uh[0]-uh[1]
order = fes.components[0].globalorder
alpha = 2
h = specialcf.mesh_size
n = specialcf.normal(mesh.dim)
a = BilinearForm(fes, **opts)
dS = dx(element_boundary=True)
a += grad(u)*grad(v)*dx + \
alpha*(order+1)**2/h*jump(uh)*jump(vh)*dS + \
(-grad(u)*n*jump(vh) - grad(v)*n*jump(uh))*dS
a.Assemble()
f = LinearForm(fes)
f += 5*v*dx
f.Assemble()
return a,f
Show code cell source
def solve_lin_system(a,f,gfu,inverse=""):
aSinv = a.mat.Inverse(gfu.space.FreeDofs(coupling=a.condense),inverse=inverse)
if a.condense:
ainv = ((IdentityMatrix(a.mat.height) + a.harmonic_extension) @ (aSinv + a.inner_solve) @ (IdentityMatrix(a.mat.height) + a.harmonic_extension_trans))
else:
ainv = aSinv
rhs = f.vec.CreateVector()
rhs.data = f.vec - a.mat * gfu.vec
gfu.vec.data += ainv * rhs
from ngsolve import *
from ngsolve.webgui import Draw
from netgen.occ import *
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
order=1
V = L2(mesh, order=order)
F = FacetFESpace(mesh, order=order, dirichlet=".*")
fes = V*F
gfu = GridFunction(fes)
a,f, = setup_HDG_system(fes, condense=True)
solve_lin_system(a,f,gfu)
Draw (gfu.components[0], mesh, "u-HDG", deformation=True);
11.4.2. Projected Jumps (and how it works)#
An observation:
\(\nabla u \! \cdot \! n \in \mathcal{P}^{k-1}(F)\) on every facet \(F\),
hence \(N_h({u}_h,\underline{v}_h) = N_h({u}_h, \Pi_{\mathcal{F}_h}^{k-1} \underline{v}_h)\) where \(\Pi_{\mathcal{F}_h}^{k-1}\) is the \(L^2(\mathcal{F}_h)\) projection on \(\mathbb{P}^{k-1}(\mathcal{F}_h)\)
We then apply the following modifications:
To bound the \(N_h\)-terms it hence suffices to reduce the stabilizing term to \(S_h^{pj}(\cdot,\cdot) = S_h^{pj}(\Pi_{\mathcal{F}_h}^{k-1}(\cdot,\cdot))\)
We hence reduce the facet space to \(\hat V_h = \mathbb{P}^{k-1}(\mathcal{F}_h)\) (which reduces the globally coupled
dofs, especially for low order methods)
Now the questions arises: How to realize the ``projected jumps’’ \(\Pi_{\mathcal{F}_h}^{k-1}(\mathcal{F}_h)\) in practice? One answer is discussed in the next section:
11.4.3. highest_order_dc: Highest order facet functions discontinuous#
The basis functions in \(\mathbb{P}^{\ell}(\mathcal{F}_h)\) ( corresponds to FacetFESpace(..., order=l, ...) in NGSolve) are constructed \(L^2\)-orthogonal (and order hierarchically).
The implementation trick for the ``projected jumps’’ method is to
use formally the same bilinear and linear form as in the standard HDG version,
but choose the following (seemingly more complicated) facet space:
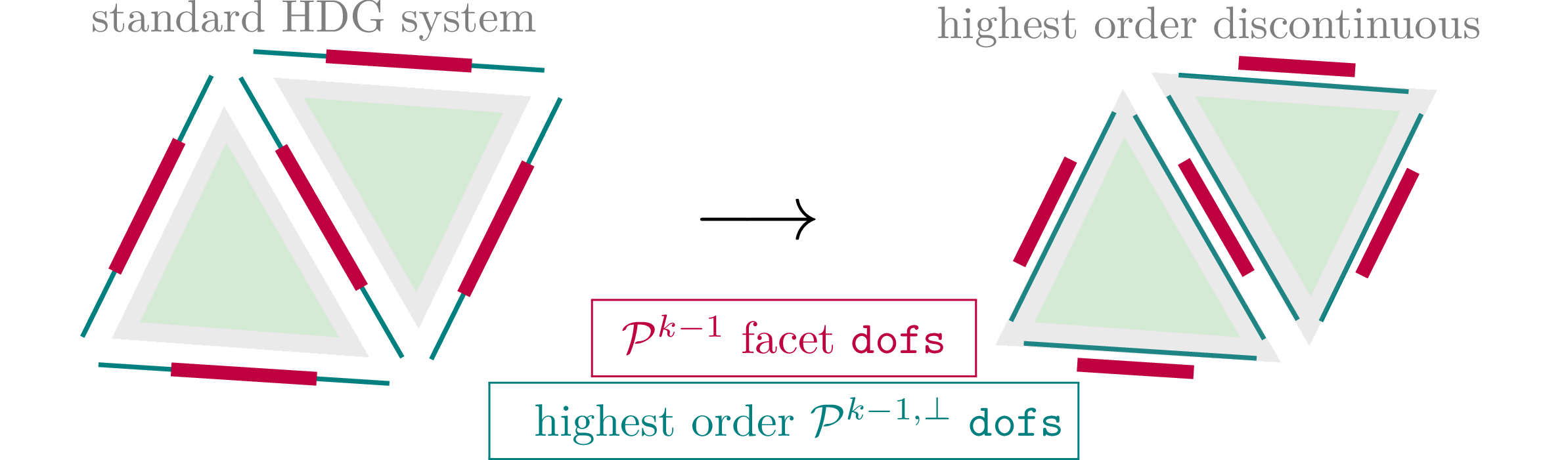
\(\hat V_h^\ast\) is to be read in the following way: Every function \(\hat v_h^\ast \in \hat V_h^\ast\) can be decomposed as \(\hat v_h^\ast = \hat v_h + \bar v_h\) where
on each facet \(F\) the \(\mathcal{P}^{k-1}(F)\)-part of the facet function, \(\hat v_h\), stays uni-valued while
the \(L^2\)-orthogonal complement in \(\mathbb{P}^{k}(F)\), \(\bar v_h\), becomes double-valued (one version for both aligned elements)
Testing with \((v_h, \hat v_h + \bar v_h) = (0,0,\bar v_h)\) with \(\bar v_h\) supported only on one facet \(F\) from one element side \(T\) in the discrete formulation we obtain only the part from the \(S_h(\cdot,\cdot)\) term (the other parts drop due to orthogonality):
Hence, the element-local facet variable becomes
We can hence eliminate \(\bar u_h\) (in dependence of \(u_h\) and \(\hat u_h\)) from the equations. Plugging it in yields the projection as on every facet \(F\) (from one side of an element \(T\)) we have:
So, in 2D we add one degree of freedom per edge:
Vhat = FacetFESpace(mesh, order=order, dirichlet=".*")
Vhats = FacetFESpace(mesh, order=order, dirichlet=".*", \
highest_order_dc=True)
print(f"Vhat.ndof = {Vhat.ndof}, Vhats.ndof = {Vhats.ndof}, difference = {Vhats.ndof - Vhat.ndof}, number of facets = {mesh.nfacet}")
Vhat.ndof = 718, Vhats.ndof = 1037, difference = 319, number of facets = 359
What is wrong? Make a guess!
The highest_order_dc-flag leaves boundary facets untouched!
Show code cell source
print(f"boundary facets: {mesh.GetNE(BND)}")
boundary facets: 40
We have introduced more unknowns, but
the new unknowns stay element-local and can be condensed out
print(f"Vhat.nfreedofs = {sum(Vhat.FreeDofs(coupling=True))}, Vhats.nfreedofs = {sum(Vhats.FreeDofs(coupling=True))}")
Vhat.nfreedofs = 638, Vhats.nfreedofs = 319
11.4.5. HDG Lifting’s#
As a next application of HIDDEN_DOFs we consider the lifting operator approach for the DG discretization.
The stability term \(S_h(\cdot,\cdot)\) in the HDG bilinear form makes up for the \(N_h(\cdot,\cdot)\)-parts that include the normal gradient on the element boundary. To obtain a more fine-grained control over this term, we can introduce a lifting operator that allows us to rewrite the stabilization term in a more flexible way:
The HDG lifting operator \(\mathcal{L}: \mathbb{P}^k(\mathcal{T}_h) \times \mathbb{P}^k(\mathcal{F}_h) \to \mathbb{P}^{k}(\mathcal{T}_h)\) is defined for \(\underline{v}_h \in V_h = V_h^T \times \hat V_h\) so that
Note that with \(w_h = w_h^0 + w_h^\perp\) and \(N_h(w_h^0, \cdot) = b_h(\cdot, w_h^) = 0\) we obtain \(\Pi^0 \mathcal{L}(\underline{v}_h) = 0\) and hence
With this we obtain:
Now, it is easy to see, that new sufficient stabilizations (without need for a sufficiently large parameter) can be designed easily.
We simply take
Note that the latter part makes it definite. Otherwise even multiples of the former part my not be sufficient if the lifting operator has a non-trivial kernel (due to a non-trivial kernel of \(N_h(\cdot,\cdot)\)), which can easily happen. Further note that the penalty term is scaled with \(\gamma k/h\) instead of \(\gamma k^2/h\) and \(\gamma > 0\) is all we need to ask for (no “sufficiently large”).
This yields
Now, for the implementation we rewrite the terms using the lifting characteristics backwards:
To implement the second-last part we introduce a new variable \(u_h^\ell = \mathcal{L}(\underline{u}_h)\) for which the lifting equality holds:
Now, Plugging \(u_h^\ell = \mathcal{L}(\underline{u}_h)\) into (A) and adding (B) yields the new formulation: Find \(\underline{\underline{u}}_h = (\underline{u}_h, u_h^\ell) \in V_h \times \mathbb{P}^{k}(\mathcal{T}_h)\) so that
def setup_lifted_HDG_system(fes, **opts):
uh, vh = fes.TnT()
order = fes.components[0].globalorder
(u,uhat,ul), (v,vhat,vl) = uh, vh
jump = lambda uh: uh[0]-uh[1]
h = specialcf.mesh_size
n = specialcf.normal(mesh.dim)
a = BilinearForm(fes, **opts)
dS = dx(element_boundary=True)
a += grad(u)*grad(v)*dx # b_h
a += (-grad(u)*n*jump(vh) - grad(v)*n*jump(uh))*dS #N_h
a += 1*(order+1)/h*jump(uh)*jump(vh)*dS # s_h
a += -grad(ul)*grad(vl)*dx # b_h (lifting)
a += (-grad(ul)*n*jump(vh) - grad(vl)*n*jump(uh))*dS #N_h (lifting)
a += - 1/(h*h)* ul * vl * dx(bonus_intorder=-2*order) # j_h
a.Assemble()
f = LinearForm(fes)
f += 5*v*dx
f.Assemble()
return a,f
We note that the new variable \(u_h^\ell\) can be treated as HIDDEN variable as
it only appears on one element
it is only needed during assembly (to realize the lifting)
the r.h.s. of the linear system for \(v_h^\ell\) is zero
We use the keyword hide_all_dofs to make all dofs in a space HIDDEN:
order=1
V = L2(mesh, order=order)
F = FacetFESpace(mesh, order=order, dirichlet=".*")
#F = Compress(FacetFESpace(mesh, order=order, dirichlet=".*", highest_order_dc=True, hide_highest_order_dc=True))
Vl = Compress(L2(mesh, order=order, hide_all_dofs=True))
fes = V*F*Vl
Is Vl empty now?
Yes and no:
print(f"global ndof: {Vl.ndof}")
for el in Vl.Elements():
print(f"local dofs on first element: {el.dofs}")
break
global ndof: 0
local dofs on first element: [-2, -2, -2]
Warning
Setting dofs as HIDDEN_DOFs changes the global number of dofs and the global numbering (after compression), but
on the element level the number of dofs is unaffected! The computation of the element matrix (before applying Schur complement strategies) is independent of any information on coupling types in the FESpace.
gfuT_vis = GridFunction(V, multidim=True)
gfu = GridFunction(fes)
for i, (opt, elims) in enumerate(reversed(linsys_opts)):
a,f, = setup_lifted_HDG_system(fes, **opt)
solve_lin_system(a,f,gfu)
print(f"condensed dofs: {elims:6}, nzes: {a.mat.nze}")
if i == 0:
gfuT_vis.vec.data = gfu.components[0].vec
else:
gfuT_vis.AddMultiDimComponent(gfu.components[0].vec)
Draw (gfuT_vis, mesh, "u-HDG", deformation=True);
condensed dofs: local, nzes: 6860
condensed dofs: hidden, nzes: 17030
condensed dofs: none, nzes: 17030
Warning
Recall: Don’t use HIDDEN_DOFs + Compress without setting condense=True or eliminate_hidden=True in the BilinearForm!
Note
Also here for the chosen lifting formulation we don’t need to penalize jumps up to order \(k\) to have a proper norm. Instead we can use the “projected jumps” approach. To try it out comment in/out the corresponding lines for Vhat above.
