This page was generated from unit-2.8-DG/DG.ipynb.

2.8 Discontinuous Galerkin Methods

• Use discontinuous finite element spaces to solve PDEs.

• Allows upwind-stabilization for convection-dominated problems

• Requires additional jump terms for consistency

Interior penalty DG form for \(-\Delta u\):

\[\DeclareMathOperator{\Div}{div} A(u,v) = \sum_T \int_T \nabla u \nabla v - \sum_F \int_F \{ n \nabla u \} [v] - \sum_F \int_F \{ n \nabla v \} [u] + \frac{\alpha p^2}{h} \sum_F \int_F [u][v]\]

with jump-term over facets:

\[[u] = u_{left} - u_{right}\]

and averaging operator

\[\{ n \nabla u \} = \tfrac{1}{2} (n_{left} \nabla u_{left} + n_{left} \nabla u_{right})\]

DG form for \(\Div (b u)\), where \(b\) is the given wind:

\[B(u,v) = -\sum_T b u \nabla v + \sum_F \int_F b\cdot n u^{upwind} v\]

from ngsolve import *
from ngsolve.webgui import Draw
mesh = Mesh(unit_square.GenerateMesh(maxh=0.3))

The space is responsible for allocating the matrix graph. Tell it that it should reserve entries for the coupling terms:

order=4
fes = L2(mesh, order=order, dgjumps=True)
u,v = fes.TnT()

Every facet has a master element. The value from the other element is referred to via the Other() operator:

jump_u = u-u.Other()
jump_v = v-v.Other()
n = specialcf.normal(2)
mean_dudn = 0.5*n * (grad(u)+grad(u.Other()))
mean_dvdn = 0.5*n * (grad(v)+grad(v.Other()))

Integrals on facets are computed by setting skeleton=True. * dx(skeleton=True) iterates over all internal faces * ds(skeleton=True) iterates over all boundary faces

alpha = 4
h = specialcf.mesh_size
diffusion = grad(u)*grad(v) * dx \
    +alpha*order**2/h*jump_u*jump_v * dx(skeleton=True) \
    +(-mean_dudn*jump_v-mean_dvdn*jump_u) * dx(skeleton=True) \
    +alpha*order**2/h*u*v * ds(skeleton=True) \
    +(-n*grad(u)*v-n*grad(v)*u)* ds(skeleton=True)

a = BilinearForm(diffusion).Assemble()

f = LinearForm(1*v*dx).Assemble()

gfu = GridFunction(fes, name="uDG")
gfu.vec.data = a.mat.Inverse() * f.vec
Draw (gfu);

DG requires a lot of additional matrix entries:

fes2 = L2(mesh, order=order)
ul2,vl2 = fes2.TnT()
a2 = BilinearForm(ul2*vl2*dx).Assemble()
print ("DG-matrix nze:", a.mat.nze)
print ("L2-matrix nze:", a2.mat.nze)

DG-matrix nze: 18900
L2-matrix nze: 5400

Next we are solving a convection-diffusion problem:

alpha = 4
h = specialcf.mesh_size

The IfPos checks whether the first argument is positive. Then it returns the second one, else the third one. This is used to define the upwind flux. The check is performed in every integration-point on the skeleton:

b = CF( (20,5) )
uup = IfPos(b*n, u, u.Other())

convection = -b * u * grad(v)*dx + b*n*uup*jump_v * dx(skeleton=True)

acd = BilinearForm(diffusion + convection).Assemble()

gfu = GridFunction(fes)
gfu.vec.data = acd.mat.Inverse(freedofs=fes.FreeDofs(),inverse="umfpack") * f.vec
Draw (gfu)

BaseWebGuiScene

Hybrid Discontinuous Galerkin methods

use additionally the hybrid facet variable on the skeleton:

\[\DeclareMathOperator{\Div}{div} A(u,\widehat u; v, \widehat v) = \sum_T \int_T \nabla u \nabla v - \sum_T \int_{\partial T} n \nabla u (v-\widehat v) - \sum_T \int_{\partial T} n \nabla v (u-\widehat u) + \frac{\alpha p^2}{h} \sum_F \int_F (u-\widehat u)(v-\widehat v)\]

the jump-term is now replaced by the difference \(u - \widehat u\).

No additional matrix entries across elements are produced. Dirichlet boundary conditions are set as usual to the facet variable:

order=4
V = L2(mesh, order=order)
F = FacetFESpace(mesh, order=order, dirichlet="bottom|left|right|top")
fes = V*F
u,uhat = fes.TrialFunction()
v,vhat = fes.TestFunction()

Now, the jump is the difference between element-term and facet-term:

jump_u = u-uhat
jump_v = v-vhat

alpha = 4
condense = True
h = specialcf.mesh_size
n = specialcf.normal(mesh.dim)

a = BilinearForm(fes, condense=condense)
dS = dx(element_boundary=True)
a += grad(u)*grad(v)*dx + \
    alpha*order**2/h*jump_u*jump_v*dS + \
    (-grad(u)*n*jump_v - grad(v)*n*jump_u)*dS

b = CF( (20,1) )
uup = IfPos(b*n, u, uhat)
a += -b * u * grad(v)*dx + b*n*uup*jump_v *dS
a.Assemble()

f = LinearForm(1*v*dx).Assemble()

gfu = GridFunction(fes)

print ("A non-zero elements:", a.mat.nze)

A non-zero elements: 4650

if not condense:
    inv = a.mat.Inverse(fes.FreeDofs(), "umfpack")
    gfu.vec.data = inv * f.vec
else:
    fmod = (f.vec + a.harmonic_extension_trans * f.vec).Evaluate()

    inv = a.mat.Inverse(fes.FreeDofs(True), "umfpack")
    gfu.vec.data = inv * fmod

    gfu.vec.data += a.harmonic_extension * gfu.vec
    gfu.vec.data += a.inner_solve * f.vec

Draw (gfu.components[0], mesh, "u-HDG");

Projected Jumps

The polynomial order of the facet-space can be reduced by one by inserting an \(L_2\)-projection into the penalty term. This can be implemented by keeping the highest order basis functions of the facet space discontinuous, see Lehrenfeld-Schöberl: High order exactly divergence-free Hybrid Discontinuous Galerkin Methods for unsteady incompressible flows:

\[\DeclareMathOperator{\Div}{div} A(u,\widehat u; v, \widehat v) = \sum_T \int_T \nabla u \nabla v - \sum_T \int_{\partial T} n \nabla u (v-\widehat v) - \sum_T \int_{\partial T} n \nabla v (u-\widehat u) + \frac{\alpha p^2}{h} \sum_F \int_F (\Pi u-\widehat u)(\Pi v-\widehat v)\]

This is achieved by setting the flag highest_order_dc=True in the FacetFESpace. The number of matrix entries is reduced, while the order of convergence is preserved. This trick does not work in the case of significant convection.

order=4
V = L2(mesh, order=order)
F = FacetFESpace(mesh, order=order, dirichlet="bottom|left|right|top", \
                          highest_order_dc=True)
fes = V*F
u,uhat = fes.TrialFunction()
v,vhat = fes.TestFunction()

jump_u = u-uhat
jump_v = v-vhat

alpha = 2
h = specialcf.mesh_size
n = specialcf.normal(mesh.dim)

a = BilinearForm(fes, condense=True)
dS = dx(element_boundary=True)
a += grad(u)*grad(v)*dx + \
    alpha*(order+1)**2/h*jump_u*jump_v*dS + \
    (-grad(u)*n*jump_v - grad(v)*n*jump_u)*dS
a.Assemble()

f = LinearForm(fes)
f += 1*v*dx
f.Assemble()

gfu = GridFunction(fes)

f.vec.data += a.harmonic_extension_trans * f.vec

inv = a.mat.Inverse(fes.FreeDofs(True), "sparsecholesky")
gfu.vec.data = inv * f.vec

gfu.vec.data += a.harmonic_extension * gfu.vec
gfu.vec.data += a.inner_solve * f.vec

Draw (gfu.components[0], mesh, "u-HDG")

print ("A non-zero elements:", a.mat.nze)

A non-zero elements: 2976

Remarks on sparsity pattern in NGSolve

Remark 1: The sparsity pattern is set up a-priorily

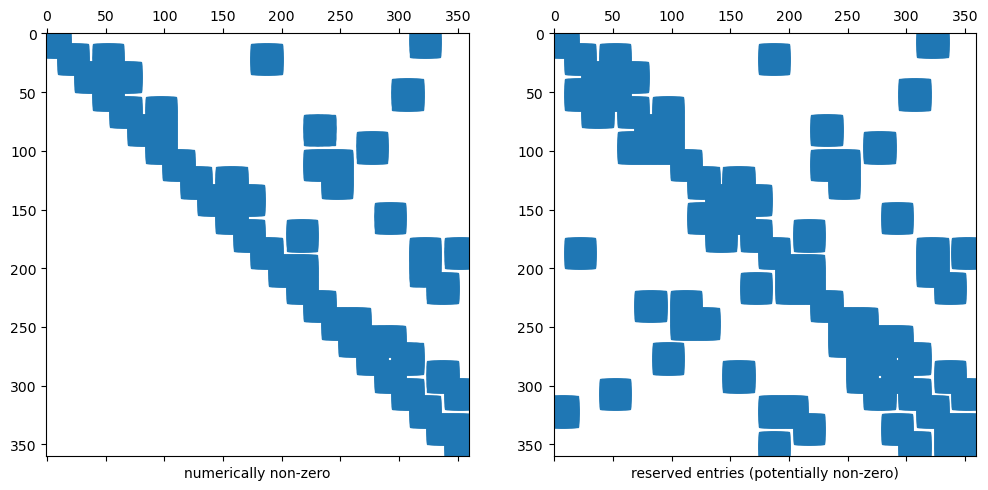
• The sparsity pattern of a sparse matrix in NGSolve is independent of its entries (it’s set up a-priorily).

• We can have "nonzero" entries that have the value 0

Below we show the reserved memory for the sparse matrix and the (numerically) non-zero entries in this sparse matrix.

fes2 = L2(mesh, order=order, dgjumps=True)
u,v=fes2.TnT()
a3 = BilinearForm(fes2)
a3 += u*v*dx + (u+u.Other())*v*dx(skeleton=True)
a3.Assemble();

import scipy.sparse as sp
import matplotlib.pylab as plt
plt.rcParams['figure.figsize'] = (12, 12)
A = sp.csr_matrix(a3.mat.CSR())
fig = plt.figure(); ax1 = fig.add_subplot(121); ax2 = fig.add_subplot(122)
ax1.set_xlabel("numerically non-zero"); ax1.spy(A)
ax2.set_xlabel("reserved entries (potentially non-zero)"); ax2.spy(A,precision=-1)
plt.show()

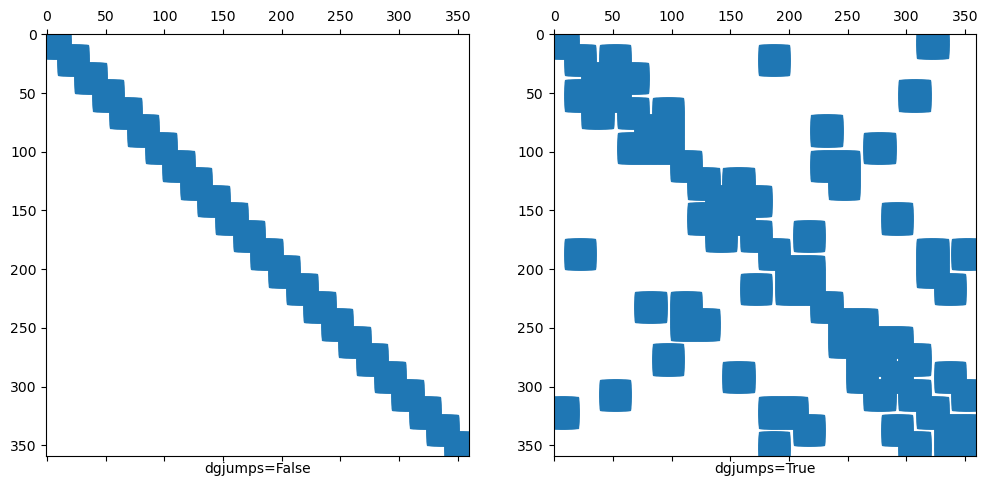
Remark 2: Sparsity pattern with and without dgjumps=True is different

a1 = BilinearForm(L2(mesh, order=order, dgjumps=False)); a1.Assemble()
a2 = BilinearForm(L2(mesh, order=order, dgjumps=True)); a2.Assemble()
A1 = sp.csr_matrix(a1.mat.CSR())
A2 = sp.csr_matrix(a2.mat.CSR())
fig = plt.figure(); ax1 = fig.add_subplot(121); ax2 = fig.add_subplot(122)
ax1.set_xlabel("dgjumps=False"); ax1.spy(A1,precision=-1)
ax2.set_xlabel("dgjumps=True"); ax2.spy(A2,precision=-1)
plt.show()

used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )
used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )

Remark 3: Dof numbering of higher order FESpaces

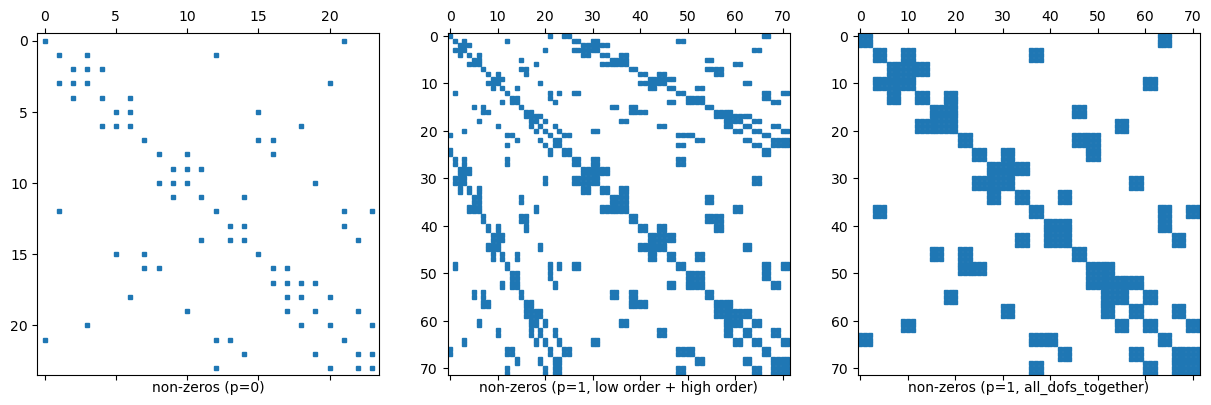
• In NGSolve FESpaces typically have a numbering where the first block of dofs corresponds to a low order subspace (which is convenient for iterative solvers).

• For L2 this means that the first dofs correspond to the constants on elements.

• You can turn this behavior off for some spaces, e.g. for L2 by adding the flag all_dofs_together.

We demonstrate this in the next comparison:

plt.rcParams['figure.figsize'] = (15, 15)
fig = plt.figure()
ax = [fig.add_subplot(131), fig.add_subplot(132), fig.add_subplot(133)]

for i, (order, all_dofs_together, label) in enumerate([(0,False, "non-zeros (p=0)"),
                                                    (1,False,"non-zeros (p=1, low order + high order)"),
                                                    (1,True,"non-zeros (p=1, all_dofs_together)")]):
    a = BilinearForm(L2(mesh,order=order,dgjumps=True,all_dofs_together=all_dofs_together))
    a.Assemble()
    ax[i].spy(sp.csr_matrix(a.mat.CSR()),markersize=3,precision=-1)
    ax[i].set_xlabel(label)

used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )
used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )
used dof inconsistency
(silence this warning by setting BilinearForm(...check_unused=False) )