This page was generated from unit-2.1.5-amg/amg.ipynb.
2.1.5 Algebraic Multigrid Methods¶
Algebraic multigrid methods (AMG) build a multigrid hierarchy from the given matrix. In contrast to geometric multigrid methods, they do not need a mesh hierarchy. Just one finite element mesh is enough.
AMG takes profit from providing the type of problem (Poisson equation, elasticity, Maxwell, …).
NGSolve comes with builtin AMG solvers for scalar equations, and for Maxwell equations. It provides also interfaces to external, parallel AMG solvers (hypre, gamg, …)
The builtin h1amg¶
The h1amg preconditioner works for symmetric, scalar problems with nodal degrees of freedom. It uses unsmoothed agglomeration for the generation of coarse spaces.
The coarsening of degrees of freedom is steered by the strength of connections between dofs, one may think of a network of resistors. For this, one finds edge-based weights \(w_E\) such that the energy norm is equivalent to the weighted sum of squared differences:
\(w_E\) is the edge-weight (the conductivity of each resistor), and \(E_1\) and \(E_2\) are the vertex numbers of the end-points of the edge \(E\). The right hand side is a norm represented by a surrogate matrix \(\tilde A\).
The first task is to determine the edge-weights \(w_E\). If one has access to element-matrices (instead of the assembled matrix), one has better possibilities. One may compute Schur complements with respect to all edges of each element, which gives a surrogate matrix for each element. Then sum up the weights (conductivities) of all elements sharing the edge.
To have access to element matrices, the setup of the surrogate matrix is included into the assembling loop. Thus, the workflow is to
define the biliear-form
define the h1amg preconditioner, which registers at the bilinear-form
finally assemble the bilinear-form, which also runs the setup of the preconditioner
[1]:
from ngsolve import *
from ngsolve.la import EigenValues_Preconditioner
# minimize memory requirements by switching off tables which we don't need here
import netgen.meshing
# currently not working
# netgen.meshing.Mesh.EnableTableClass("edges", False)
# netgen.meshing.Mesh.EnableTableClass("faces", False)
with TaskManager():
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.1))
for l in range(3): mesh.Refine()
[2]:
# fes = H1(mesh, order=1, order_policy=ORDER_POLICY.CONSTANT) # todo: fix withtout edge/face tables
fes = FESpace("nodal", mesh, order=1)
print ("ndof=", fes.ndof)
u,v = fes.TnT()
a = BilinearForm(grad(u)*grad(v)*dx + 1e-3*u*v*dx)
pre = Preconditioner(a, "h1amg")
with TaskManager():
a.Assemble();
lam = EigenValues_Preconditioner(a.mat, pre.mat)
print (list(lam[0:3]), '...', list(lam[-3:-1]))
ndof= 431209
[0.18404791677244126, 0.20767372819972618, 0.24444169860638254] ... [0.9653063480316779, 0.9928328276489375]
H(curl) - AMG¶
The hcurlamg is an implementation of the amg from Reitzinger and Schöberl: An algebraic multigrid method for finite element discretizations with edge elements.
It is based on a surrogate matrix for a weighted \(H(\operatorname{curl})\) norm discretized by lowest order Nedelec elements:
The smoother is a Hiptmair smoother, where a Gauss-Seidel smoother is combined with another Gauss-Seidel smoother for the potential space.
The key is a coarsening which preserves the de Rham sequence over all levels, such that Hiptmair’s smoother is effective also on coarser levels.
More recent, robust coarsening strategies are developed in B. Schwarzenbacher: Robust algebraic solvers for electromagnetics, Master’s Thesis
[3]:
from ngsolve import *
from ngsolve.la import EigenValues_Preconditioner
# switch on again generation of tables
import netgen.meshing
netgen.meshing.Mesh.EnableTableClass("edges", True)
netgen.meshing.Mesh.EnableTableClass("faces", True)
with TaskManager():
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.1))
for l in range(1): mesh.Refine()
[4]:
fes = HCurl(mesh, order=0)
print ("ndof = ", fes.ndof)
u,v = fes.TnT()
a = BilinearForm(curl(u)*curl(v)*dx + 0.01*u*v*dx)
pre = Preconditioner(a, "hcurlamg")
with TaskManager():
a.Assemble()
lam = EigenValues_Preconditioner(a.mat, pre.mat)
print (list(lam[0:3]), '...', list(lam[-3:-1]))
ndof = 55653
[0.09009990782723559, 0.10749838234081349, 0.14164780309913066] ... [0.9793704192046186, 0.9939509121546828]
[5]:
f = LinearForm(curl(v)[2]*dx).Assemble()
gfu = GridFunction(fes)
from ngsolve.krylovspace import CGSolver
inv = CGSolver(a.mat, pre.mat, plotrates=False, maxiter=200)
gfu.vec[:] = inv*f.vec
A simple coil:¶
[6]:
from ngsolve import *
from netgen.occ import *
from ngsolve.webgui import Draw, FieldLines
[7]:
coil = Cylinder(Axes((0,0,-0.4),Z), r=0.4, h=0.8) - \
Cylinder(Axes((0,0,-0.4),Z), r=0.2, h=0.8)
coil.solids.name="coil"
coil.faces.col=(1,0,0)
coil.faces.maxh=0.04
box = Box((-2,-2,-2), (2,2,2) )
box.faces.col=(0,0,1, 0.5)
box.faces.name="outer"
air = box-coil
air.solids.name="air"
shape = Glue([coil,air])
ea = { "euler_angles" : (-60, 0, -11) }
Draw (shape, **ea);
[8]:
with TaskManager():
mesh = Mesh(OCCGeometry(shape).GenerateMesh(maxh=0.3)).Curve(5)
for l in range(1):
mesh.Refine()
The variational formulation for the magnetic vector-potential is: find \(u \in H(\operatorname{curl})\)
[9]:
fes = HCurl(mesh, order=0)
print ("ndof = ", fes.ndof)
u,v = fes.TnT()
mu = 4*pi*1e-7
a = BilinearForm(1/mu*curl(u)*curl(v)*dx + 1e-6/mu*u*v*dx)
pre = preconditioners.HCurlAMG(a, verbose=2, smoothingsteps=3, smoothedprolongation=True, maxcoarse=10,
maxlevel=10, potentialsmoother='amg')
with TaskManager():
a.Assemble()
ndof = 670489
Create AMG matrix
smoothingsteps = 3
smoothedprolongation = 1
maxcoarse = 10
maxlevel = 10
setup level 0, matsize = 670489, nedge = 670489, nface = 1011484
setup level 1, matsize = 101583, nedge = 101583, nface = 177398
setup level 2, matsize = 16835, nedge = 16835, nface = 30862
setup level 3, matsize = 2685, nedge = 2685, nface = 5400
setup level 4, matsize = 334, nedge = 334, nface = 738
setup level 5, matsize = 20, nedge = 20, nface = 28
coarse direct inverse, size = 6
[10]:
from ngsolve.la import EigenValues_Preconditioner
with TaskManager():
lam = EigenValues_Preconditioner(a.mat, pre)
print (list(lam[0:3]), list(lam[-3:]))
[0.11678948216443163, 0.1753956117394127, 0.22782182938998846] [0.9754614763421057, 0.9927278163394353, 0.9999304139234781]
The current in the coil consisting of many turns is modeled as homogeneous current density:
with number of turns \(N\), current \(I\), coil crosssection \(A\), and \(\tau\) is a normalized vectorfield in azimuthal direction.
[11]:
tau = CF((y,-x,0))
tau = tau/Norm(tau)
N = 1000 # turns
I = 1 # current
crosssection = 0.2*0.8
j = N*I/crosssection
f = LinearForm(j*tau*v*dx("coil", bonus_intorder=6)).Assemble()
[12]:
gfu = GridFunction(fes)
with TaskManager():
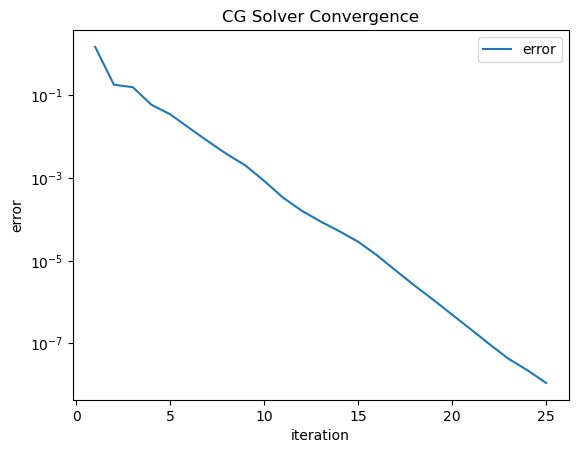
inv = solvers.CGSolver(a.mat, pre.mat, tol=1e-8, maxiter=100, plotrates=True)
gfu.vec.data = inv*f.vec
<Figure size 640x480 with 0 Axes>
[13]:
ea = { "euler_angles" : (-60, 0, -11) }
clipping = { "clipping" : { "y":1, "z":0, "dist":0.5} }
fieldlines = FieldLines(curl(gfu), mesh.Materials(".*"), length=2, num_lines=100)
Draw(curl(gfu), mesh, "X", draw_vol=False, draw_surf=True, objects=[fieldlines], \
min=0, max=5e-4, autoscale=False, settings={"Objects": {"Surface": False, "Wireframe": False}}, **ea);
[ ]: