This page was generated from unit-2.1.4-bddc/bddc.ipynb.

2.1.4 Element-wise BDDC Preconditioner

The element-wise BDDC (Balancing Domain Decomposition preconditioner with Constraints) preconditioner in NGSolve is a good general purpose preconditioner that works well both in the shared memory parallel mode as well as in distributed memory mode. In this tutorial, we discuss this preconditioner, related built-in options, and customization from python.

Let us start with a simple description of the element-wise BDDC in the context of Lagrange finite element space \(V\). Here the BDDC preconditioner is constructed on an auxiliary space \(\widetilde{V}\) obtained by connecting only element vertices (leaving edge and face shape functions discontinuous). Although larger, the auxiliary space allows local elimination of edge and face variables. Hence an analogue of the original matrix \(A\) on this space, named \(\widetilde A\), is less expensive to invert. This inverse is used to construct a preconditioner for \(A\) as follows:

\[C_{BDDC}^{-1} = R {\,\widetilde{A}\,}^{-1}\, R^t\]

Here, \(R\) is the averaging operator for the discontinuous edge and face variables.

To construct a general purpose BDDC preconditioner, NGSolve generalizes this idea to all its finite element spaces by a classification of degrees of freedom. Dofs are classified into (condensable) LOCAL_DOFs that we saw in 1.4 and a remainder that includes these types:

WIREBASKET_DOF
INTERFACE_DOF

The original finite element space \(V\) is obtained by requiring conformity of both the above types of dofs, while the auxiliary space \(\widetilde{V}\) is obtained by requiring conformity of WIREBASKET_DOFs only.

Here is a figure of a typical function in the default \(\widetilde{V}\) (and the code to generate this is at the end of this tutorial) when \(V\) is the Lagrange space:

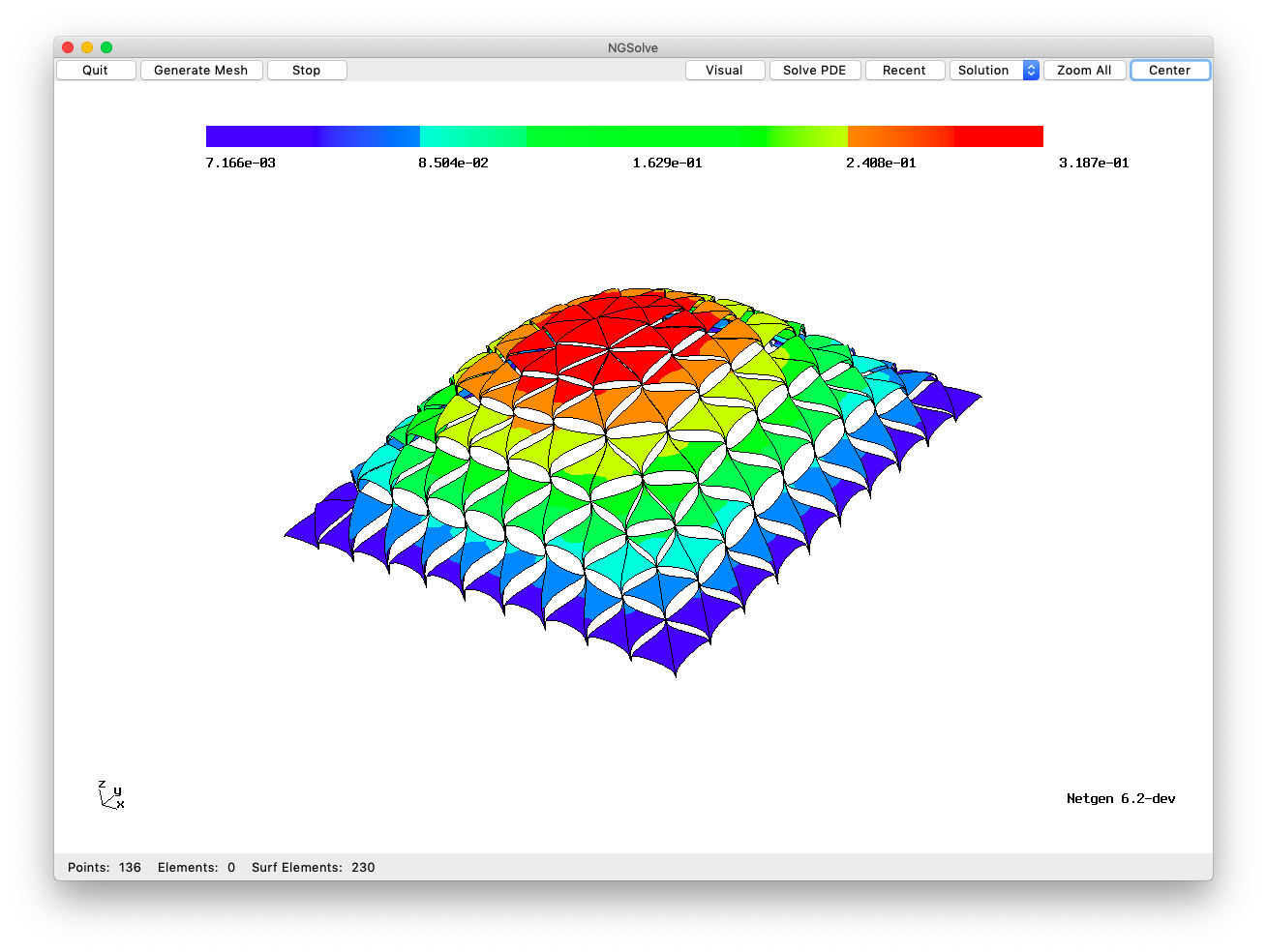
title 
[1]:

from ngsolve import *
from ngsolve.webgui import Draw
from ngsolve.la import EigenValues_Preconditioner
SetHeapSize(100*1000*1000)

[2]:

mesh = Mesh(unit_cube.GenerateMesh(maxh=0.5))
# mesh = Mesh(unit_square.GenerateMesh(maxh=0.5))

Built-in options

Let us define a simple function to study how the spectrum of the preconditioned matrix changes with various options.

Effect of condensation

[3]:

def TestPreconditioner (p, condense=False, **args):
    fes = H1(mesh, order=p, **args)
    u,v = fes.TnT()
    a = BilinearForm(fes, eliminate_internal=condense)
    a += grad(u)*grad(v)*dx + u*v*dx
    c = Preconditioner(a, "bddc")
    a.Assemble()
    return EigenValues_Preconditioner(a.mat, c.mat)

[4]:

lams = TestPreconditioner(5)
print (lams[0:3], "...\n", lams[-3:])

 1.00052
 1.03338
 1.09991
 ...
  4.55515
 4.60067
 4.79194

Here is the effect of static condensation on the BDDC preconditioner.

[5]:

lams = TestPreconditioner(5, condense=True)
print (lams[0:3], "...\n", lams[-3:])

 1.00023
 1.02753
 1.08363
 ...
  4.06546
 4.12581
 4.22957

Tuning the auxiliary space

Next, let us study the effect of a few built-in flags for finite element spaces that are useful for tweaking the behavior of the BDDC preconditioner. The effect of these flags varies in two (2D) and three dimensions (3D), e.g.,

  • wb_fulledges=True: This option keeps all edge-dofs conforming (i.e. they are marked WIREBASKET_DOFs). This option is only meaningful in 3D. If used in 2D, the preconditioner becomes a direct solver.

  • wb_withedges=True: This option keeps only the first edge-dof conforming (i.e., the first edge-dof is marked WIREBASKET_DOF and the remaining edge-dofs are marked INTERFACE_DOFs).

The complete situation is a bit more complex due to the fact these options can take the three values True, False, or Undefined, the two options can be combined, and the space dimension can be 2 or 3. The default value of these flags in NGSolve is Undefined. Here is a table with the summary of the effect of these options:

wb_fulledges

wb_withedges

2D

3D

True

any value

all

all

False/Undefined

Undefined

none

first

False/Undefined

False

none

none

False/Undefined

True

first

first

An entry \(X \in\) {all, none, first} of the last two columns is to be read as follows: \(X\) of the edge-dofs is(are) WIREBASKET_DOF(s).

Here is an example of the effect of one of these flag values.

[6]:

lams = TestPreconditioner(5, condense=True,
                          wb_withedges=False)
print (lams[0:3], "...\n", lams[-3:])

 1.00106
 1.07035
 1.22031
 ...
  25.4058
  25.406
 26.9095

Clearly, when moving from the default case (where the first of the edge dofs are wire basket dofs) to the case (where none of the edge dofs are wire basket dofs), the conditioning became less favorable.

Customize

From within python, we can change the types of degrees of freedom of finite element spaces, thus affecting the behavior of the BDDC preconditioner.

To depart from the default and commit the first two edge dofs to wire basket, we perform the next steps:

[7]:

fes = H1(mesh, order=10)
u,v = fes.TnT()

for ed in mesh.edges:
    dofs = fes.GetDofNrs(ed)
    for d in dofs:
        fes.SetCouplingType(d, COUPLING_TYPE.INTERFACE_DOF)

    # Set the first two edge dofs to be conforming
    fes.SetCouplingType(dofs[0], COUPLING_TYPE.WIREBASKET_DOF)
    fes.SetCouplingType(dofs[1], COUPLING_TYPE.WIREBASKET_DOF)

a = BilinearForm(fes, eliminate_internal=True)
a += grad(u)*grad(v)*dx + u*v*dx
c = Preconditioner(a, "bddc")
a.Assemble()

lams=EigenValues_Preconditioner(a.mat, c.mat)
max(lams)/min(lams)

[7]:

9.989385160527986

This is a slight improvement from the default.

[8]:

lams = TestPreconditioner (10, condense=True)
max(lams)/min(lams)

[8]:

13.974958344240997

Combine BDDC with AMG for large problems

The coarse inverse \({\,\widetilde{A}\,}^{-1}\) of BDDC is expensive on fine meshes. Using the option coarsetype=h1amg flag, we can ask BDDC to replace \({\,\widetilde{A}\,}^{-1}\) by an Algebraic MultiGrid (AMG) preconditioner. Since NGSolve’s h1amg is well-suited
for the lowest order Lagrange space, we use the option wb_withedges=False to ensure that \(\widetilde{A}\) is made solely with vertex unknowns.
[9]:

p = 5
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.05))
fes = H1(mesh, order=p, dirichlet="left|bottom|back",
         wb_withedges=False)
print("NDOF = ", fes.ndof)
u,v = fes.TnT()
a = BilinearForm(fes)
a += grad(u)*grad(v)*dx
f = LinearForm(fes)
f += v*dx

with TaskManager():
    pre = Preconditioner(a, "bddc", coarsetype="h1amg")
    a.Assemble()
    f.Assemble()

    gfu = GridFunction(fes)
    solvers.CG(mat=a.mat, rhs=f.vec, sol=gfu.vec,
               pre=pre, maxsteps=500)
Draw(gfu)

NDOF =  746336
CG iteration 1, residual = 0.7291770014214167
CG iteration 2, residual = 0.3085825766635181
CG iteration 3, residual = 0.2751732227805908
CG iteration 4, residual = 0.314714587389768
CG iteration 5, residual = 0.3259131004628558
CG iteration 6, residual = 0.23576504582611504
CG iteration 7, residual = 0.19398509258723357
CG iteration 8, residual = 0.1717230096131164
CG iteration 9, residual = 0.12859873356543539
CG iteration 10, residual = 0.0937315719812053
CG iteration 11, residual = 0.06655712957878449
CG iteration 12, residual = 0.05174938893736049
CG iteration 13, residual = 0.04172415751108716
CG iteration 14, residual = 0.032023490025171165
CG iteration 15, residual = 0.02426903728316403
CG iteration 16, residual = 0.018659350366406355
CG iteration 17, residual = 0.014925202785173432
CG iteration 18, residual = 0.011465515055233187
CG iteration 19, residual = 0.008563421986446659
CG iteration 20, residual = 0.006510717807331378
CG iteration 21, residual = 0.0049904387622432215
CG iteration 22, residual = 0.00388553777211935
CG iteration 23, residual = 0.002883633564280205
CG iteration 24, residual = 0.0021959004578735617
CG iteration 25, residual = 0.0016985067526936847
CG iteration 26, residual = 0.0013046513241761265
CG iteration 27, residual = 0.0010193922821230155
CG iteration 28, residual = 0.0007914753128957838
CG iteration 29, residual = 0.000610114609062026
CG iteration 30, residual = 0.0004683778064138056
CG iteration 31, residual = 0.00036001776133060643
CG iteration 32, residual = 0.0002705004013187808
CG iteration 33, residual = 0.00020840307881339571
CG iteration 34, residual = 0.00016312455042230065
CG iteration 35, residual = 0.00012583355270539304
CG iteration 36, residual = 0.00010136588804030689
CG iteration 37, residual = 9.667539630164683e-05
CG iteration 38, residual = 6.90658167518186e-05
CG iteration 39, residual = 5.109289097840415e-05
CG iteration 40, residual = 3.8524754923787056e-05
CG iteration 41, residual = 2.925713051322649e-05
CG iteration 42, residual = 2.2664682620569088e-05
CG iteration 43, residual = 1.7715665630312966e-05
CG iteration 44, residual = 1.5512152054230782e-05
CG iteration 45, residual = 1.2885037114465716e-05
CG iteration 46, residual = 9.024573199578485e-06
CG iteration 47, residual = 6.748509020210403e-06
CG iteration 48, residual = 5.283699332921452e-06
CG iteration 49, residual = 4.083469803018917e-06
CG iteration 50, residual = 3.139451285063085e-06
CG iteration 51, residual = 2.4284704466364058e-06
CG iteration 52, residual = 1.8721963143901148e-06
CG iteration 53, residual = 1.4390437182173477e-06
CG iteration 54, residual = 1.0843558896857438e-06
CG iteration 55, residual = 8.218784873680402e-07
CG iteration 56, residual = 6.348404559102587e-07
CG iteration 57, residual = 4.888231967335967e-07
CG iteration 58, residual = 3.7460441893488436e-07
CG iteration 59, residual = 2.914325585096923e-07
CG iteration 60, residual = 2.2724058816885915e-07
CG iteration 61, residual = 1.7145434744135624e-07
CG iteration 62, residual = 1.311809392837606e-07
CG iteration 63, residual = 1.0169791769763315e-07
CG iteration 64, residual = 7.931693631775745e-08
CG iteration 65, residual = 6.139245754092763e-08
CG iteration 66, residual = 5.0444666557005933e-08
CG iteration 67, residual = 4.809934385417316e-08
CG iteration 68, residual = 3.367248635568807e-08
CG iteration 69, residual = 2.4703351825025247e-08
CG iteration 70, residual = 1.8764150589434895e-08
CG iteration 71, residual = 1.448674126230018e-08
CG iteration 72, residual = 1.1245291507693783e-08
CG iteration 73, residual = 8.62057102876595e-09
CG iteration 74, residual = 6.808088126122667e-09
CG iteration 75, residual = 5.484043548334304e-09
CG iteration 76, residual = 4.421363967339219e-09
CG iteration 77, residual = 3.388496851311695e-09
CG iteration 78, residual = 2.960341258713965e-09
CG iteration 79, residual = 2.3469850662862317e-09
CG iteration 80, residual = 1.7054085942848325e-09
CG iteration 81, residual = 1.2955046527692058e-09
CG iteration 82, residual = 9.927943265033497e-10
CG iteration 83, residual = 7.680326825748241e-10
CG iteration 84, residual = 5.89050442119029e-10
CG iteration 85, residual = 4.581635199589333e-10
CG iteration 86, residual = 3.550833472167561e-10
CG iteration 87, residual = 2.678216961645832e-10
CG iteration 88, residual = 2.0437759151739657e-10
CG iteration 89, residual = 1.5803762482637404e-10
CG iteration 90, residual = 1.2138032994666233e-10
CG iteration 91, residual = 9.268118027564158e-11
CG iteration 92, residual = 7.117924857911955e-11
CG iteration 93, residual = 5.4385932786852414e-11
CG iteration 94, residual = 4.261748316596259e-11
CG iteration 95, residual = 4.0163173743497506e-11
CG iteration 96, residual = 3.1818109392018115e-11
CG iteration 97, residual = 2.280256859221823e-11
CG iteration 98, residual = 1.7956744258644695e-11
CG iteration 99, residual = 1.4211777854979844e-11
CG iteration 100, residual = 1.0975926279590484e-11
CG iteration 101, residual = 8.214119188796779e-12
CG iteration 102, residual = 6.263077542664754e-12
CG iteration 103, residual = 4.827200181648033e-12
CG iteration 104, residual = 3.703268927549807e-12
CG iteration 105, residual = 2.8246780876458675e-12
CG iteration 106, residual = 2.1334392956633334e-12
CG iteration 107, residual = 1.614407821170975e-12
CG iteration 108, residual = 1.2264305923631955e-12
CG iteration 109, residual = 9.476912061410503e-13
CG iteration 110, residual = 7.956605382918463e-13
CG iteration 111, residual = 7.17109799040383e-13

[9]:

BaseWebGuiScene

Postscript

By popular demand, here is the code to draw the figure found at the beginning of this tutorial:

[10]:

from netgen.geom2d import unit_square
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
fes_ho = Discontinuous(H1(mesh, order=10))
fes_lo = H1(mesh, order=1, dirichlet=".*")
fes_lam = Discontinuous(H1(mesh, order=1))
fes = fes_ho*fes_lo*fes_lam
uho, ulo, lam = fes.TrialFunction()

a = BilinearForm(fes)
a += Variation(0.5 * grad(uho)*grad(uho)*dx
               - 1*uho*dx
               + (uho-ulo)*lam*dx(element_vb=BBND))
gfu = GridFunction(fes)
solvers.Newton(a=a, u=gfu)
Draw(gfu.components[0],deformation=True, settings={"camera": {"transformations": [{"type": "rotateX", "angle": -45}]}})

Newton iteration  0
err =  0.39346141669995033
Newton iteration  1
err =  2.4388275071858333e-15

[10]:

BaseWebGuiScene