This page was generated from unit-2.10-dualbasis/dualbasis.ipynb.

2.10 Dual basis functions¶

We use dual basis functions to define interpolation operators, define transfer operators between different finite element spaces, and auxiliary space preconditioners.

Canonical interpolation¶

The canonical finite element interpolation operator is defined by specifying the degrees of freedom. For low order methods these are typically nodal values, while for high order methods these are most often moments. For example, the interpolation of a function \(u\) onto the \(p^{th}\) order triangle is given by: find \(u_{hp} \in V_{hp}\) such that

\begin{eqnarray*} u_{hp} (V) & = & u(V) \quad \forall \text{ vertices } V \\ \int_E u_{hp} q & = & \int_E u q \quad \forall q \in P^{p-2}(E) \; \forall \text{ edges } E \\ \int_T u_{hp} q & = & \int_T u q \quad \forall q \in P^{p-3}(T) \; \forall \text{ triangles } T \end{eqnarray*}

[1]:

from ngsolve import *
from ngsolve.webgui import Draw

import matplotlib.pylab as plt
mesh = Mesh(unit_square.GenerateMesh(maxh=2))

The NGSolve 'Set' function does local projection, and simple averaging. In particular, this does not respect point values in mesh vertices.

[2]:

fes = H1(mesh, order=3, low_order_space=False)

func = x*x*x*x
gfu = GridFunction(fes)
gfu.Set(func)
Draw (gfu)
print (gfu.vec)

 -0.0223792
 0.991843
 0.977621
 -0.00815655
 3.34984
 2.19912
 3.34984
       2
 0.00660131
 1.39013e-14
 0.00660131
 -3.19744e-14
 3.34984
 -1.80088
 -2.17601
 1.82399

Most NGSolve finite element spaces provide now a "dual" operator, which delivers the moments (i.e. the dual space basis functions) instead of function values. The integrals over faces, edges and also vertices are defined by co-dimension 1 (=BND), co-dimension 2 (=BBND) or co-dimension 3 (=BBBND) integrals over the volume elements. We define a variational problem for canonical interpolation:

[3]:

u,v = fes.TnT()
vdual = v.Operator("dual")

a = BilinearForm(fes)
a += u*vdual*dx + u*vdual*dx(element_vb=BND) + \
    u*vdual*dx(element_vb=BBND)
a.Assemble()

f = LinearForm(fes)
f += func*vdual*dx + func*vdual*dx(element_vb=BND) + \
    func*vdual*dx(element_vb=BBND)
f.Assemble()

# interpolation in vertices preserves values 0 and 1
gfu.vec.data = a.mat.Inverse() * f.vec
print (gfu.vec)
Draw (gfu);

       0
       1
       1
       0
     3.6
       2
     3.6
       2
       0
       0
 -6.93335e-32
 -1.66533e-15
     3.6
      -2
      -2
       2

The vertex degrees of freedom vanish for edge and element basis functions, and the edge degrees of freedom vanish for element basis functions, but not vice-versa. Thus, the obtained matrix A is block-triangular:

[4]:

import scipy.sparse as sp
A = sp.csr_matrix(a.mat.CSR())
plt.rcParams['figure.figsize'] = (4,4)
plt.spy(A)
plt.show()

/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.4
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

../../_images/i-tutorials_unit-2.10-dualbasis_dualbasis_8_1.png

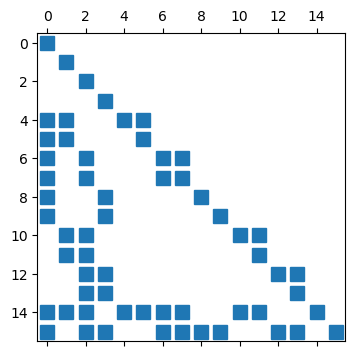
We can use proper block Gauss-Seidel smoothing for solving with that block triangular matrix by blocking the dofs for the individual vertices, edges and elements. Since the NGSolve Gauss-Seidel smoother reorders the order of smoothing blocks for parallelization, we have to take care to first compute vertex values, then edge values, and finally element values by running three different Gauss-Seidel sweeps.

[5]:

vblocks = [fes.GetDofNrs(vertex) for vertex in mesh.vertices]
eblocks = [fes.GetDofNrs(edge) for edge in mesh.edges]
fblocks = [fes.GetDofNrs(face) for face in mesh.faces]

print (vblocks)
print (eblocks)
print (fblocks)

vinv = a.mat.CreateBlockSmoother(vblocks)
einv = a.mat.CreateBlockSmoother(eblocks)
finv = a.mat.CreateBlockSmoother(fblocks)

vinv.Smooth(gfu.vec, f.vec)
einv.Smooth(gfu.vec, f.vec)
finv.Smooth(gfu.vec, f.vec)
print (gfu.vec)

[(0,), (1,), (2,), (3,)]
[(4, 5), (6, 7), (8, 9), (10, 11), (12, 13)]
[(14,), (15,)]
       0
       1
       1
       0
     3.6
       2
     3.6
       2
       0
       0
 -6.93335e-32
 -1.66533e-15
     3.6
      -2
      -2
       2

Embedding Finite Element Spaces¶

This interpolation can be used to transform functions from one finite element space \(V_{src}\) to another one \(V_{dst}\). We use the dual space of the destination space:

\[\int_{node} u_{dst} v_{dual} = \int_{node} u_{src} v_{dual} \qquad \forall \, v_{dual} \; \forall \, \text{nodes}\]

The left hand side leads to a non-symmetric square matrix, the right hand side to a rectangular matrix.

As an example we implement the transformation from an vector valued \(H^1\) space into \(H(\operatorname{div})\):

[6]:

from ngsolve import *
from ngsolve.webgui import Draw
from netgen.geom2d import unit_square
mesh = Mesh(unit_square.GenerateMesh(maxh=0.2))

fesh1 = VectorH1(mesh, order=2)
feshdiv = HDiv(mesh, order=2)

gfuh1 = GridFunction(fesh1)
gfuh1.Set ( (x*x,y*y) )

gfuhdiv = GridFunction(feshdiv, name="uhdiv")

Build the matrices, and use a direct solver:

[7]:

amixed = BilinearForm(trialspace=fesh1, testspace=feshdiv)
ahdiv = BilinearForm(feshdiv)

u,v = feshdiv.TnT()
vdual = v.Operator("dual")
uh1 = fesh1.TrialFunction()

dS = dx(element_boundary=True)
ahdiv += u*vdual * dx + u*vdual * dS
ahdiv.Assemble()

amixed += uh1*vdual*dx + uh1*vdual*dS
amixed.Assemble()

# build transformation operator:
transform = ahdiv.mat.Inverse() @ amixed.mat
gfuhdiv.vec.data = transform * gfuh1.vec

Draw (gfuh1)
Draw (gfuhdiv)

[7]:

BaseWebGuiScene

We implement a linear operator performing the fast conversion by Gauss-Seidel smoothing:

[8]:

class MyBlockInverse(BaseMatrix):
    def __init__ (self, mat, eblocks, fblocks):
        super(MyBlockInverse, self).__init__()
        self.mat = mat
        self.einv = mat.CreateBlockSmoother(eblocks)
        self.finv = mat.CreateBlockSmoother(fblocks)
        self.res = self.mat.CreateColVector()

    def CreateRowVector(self):
        return self.mat.CreateColVector()
    def CreateColVector(self):
        return self.mat.CreateRowVector()

    def Mult(self, x, y):
        # y[:] = 0
        # self.einv.Smooth(y,x)    #   y = y +  A_E^-1  (x - A y)
        # self.finv.Smooth(y,x)    #   y = y +  A_E^-1  (x - A y)

        # the same, but we see how to transpose that
        y.data = self.einv * x
        self.res.data = x - self.mat * y
        y.data += finv * self.res

    def MultTrans(self, x, y):
        y.data = self.finv.T * x
        self.res.data = x - self.mat.T * y
        y.data += einv.T * self.res


eblocks = [feshdiv.GetDofNrs(edge) for edge in mesh.edges]
fblocks = [feshdiv.GetDofNrs(face) for face in mesh.faces]

transform = MyBlockInverse(ahdiv.mat, eblocks, fblocks) @ amixed.mat
gfuhdiv.vec.data = transform * gfuh1.vec

Auxiliary Space Preconditioning¶

Nepomnyaschikh 91, Hiptmair-Xu 07, ….

Assume we have a complicated problem with some complicated discretization, and we have good preconditioners for a nodal finite element discretization for the Laplace operator. By auxiliary space preconditioning we can reuse the simple preconditioners for the complicated problems. It is simple, and works well in many cases.

As a simple example, we precondition a DG discretization by an \(H^1\) conforming method.

[9]:

mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))

The DG discretization:

[10]:

order=4
fesDG = L2(mesh, order=order, dgjumps=True)
u,v = fesDG.TnT()
aDG = BilinearForm(fesDG)
jump_u = u-u.Other()
jump_v = v-v.Other()
n = specialcf.normal(2)
mean_dudn = 0.5*n * (grad(u)+grad(u.Other()))
mean_dvdn = 0.5*n * (grad(v)+grad(v.Other()))
alpha = 4
h = specialcf.mesh_size
aDG = BilinearForm(fesDG)
aDG += grad(u)*grad(v) * dx
aDG += alpha*order**2/h*jump_u*jump_v * dx(skeleton=True)
aDG += alpha*order**2/h*u*v * ds(skeleton=True)
aDG += (-mean_dudn*jump_v -mean_dvdn*jump_u) * dx(skeleton=True)
aDG += (-n*grad(u)*v-n*grad(v)*u)* ds(skeleton=True)
aDG.Assemble()

fDG = LinearForm(fesDG)
fDG += 1*v * dx
fDG.Assemble()
gfuDG = GridFunction(fesDG)

The auxiliary \(H^1\) discretization:

[11]:

fesH1 = H1(mesh, order=2, dirichlet=".*")
u,v = fesH1.TnT()
aH1 = BilinearForm(fesH1)
aH1 += grad(u)*grad(v)*dx
preH1 = Preconditioner(aH1, "bddc")
aH1.Assemble()

[11]:

<ngsolve.comp.BilinearForm at 0x7f114cc47270>

[12]:

transform = fesH1.ConvertL2Operator(fesDG)
pre = transform @ preH1.mat @ transform.T + aDG.mat.CreateSmoother()

solvers.CG(mat=aDG.mat, rhs=fDG.vec, sol=gfuDG.vec, pre=pre, \
           maxsteps=200)

Draw (gfuDG)

CG iteration 1, residual = 0.2532119733219237
CG iteration 2, residual = 0.032832421483037784
CG iteration 3, residual = 0.008130862525680696
CG iteration 4, residual = 0.0034342488110602224
CG iteration 5, residual = 0.0011783456811530347
CG iteration 6, residual = 0.0009046659695335689
CG iteration 7, residual = 0.0009161002088522174
CG iteration 8, residual = 0.0010697558880604526
CG iteration 9, residual = 0.0007971399933259374
CG iteration 10, residual = 0.0006627896366674143
CG iteration 11, residual = 0.0005095344857658818
CG iteration 12, residual = 0.00042466444937132883
CG iteration 13, residual = 0.0003261702302928003
CG iteration 14, residual = 0.0003439552949808913
CG iteration 15, residual = 0.00027105251267776497
CG iteration 16, residual = 0.00023336881656180745
CG iteration 17, residual = 0.00017983771681640435
CG iteration 18, residual = 0.00013566763832044843
CG iteration 19, residual = 8.969965836308269e-05
CG iteration 20, residual = 7.588906438782407e-05
CG iteration 21, residual = 6.938043743084399e-05
CG iteration 22, residual = 6.381887596483356e-05
CG iteration 23, residual = 5.180208019108472e-05
CG iteration 24, residual = 4.3817631293676836e-05
CG iteration 25, residual = 3.6407249876794426e-05
CG iteration 26, residual = 2.9808360832852184e-05
CG iteration 27, residual = 2.9223985181307534e-05
CG iteration 28, residual = 2.908952039243142e-05
CG iteration 29, residual = 2.6390001567258753e-05
CG iteration 30, residual = 2.04424462466682e-05
CG iteration 31, residual = 1.7799471861373383e-05
CG iteration 32, residual = 1.4280353976732307e-05
CG iteration 33, residual = 1.1724086434440639e-05
CG iteration 34, residual = 1.0399082092347814e-05
CG iteration 35, residual = 9.35745025458749e-06
CG iteration 36, residual = 8.046132496256356e-06
CG iteration 37, residual = 6.434972748061869e-06
CG iteration 38, residual = 4.9774230748043e-06
CG iteration 39, residual = 4.189516701918543e-06
CG iteration 40, residual = 3.879825859447493e-06
CG iteration 41, residual = 3.4249941633554078e-06
CG iteration 42, residual = 3.1039505254082816e-06
CG iteration 43, residual = 2.6848114735437898e-06
CG iteration 44, residual = 2.1289592891352334e-06
CG iteration 45, residual = 1.7175875308399824e-06
CG iteration 46, residual = 1.5033515289258826e-06
CG iteration 47, residual = 1.494495426696724e-06
CG iteration 48, residual = 1.4120180027628202e-06
CG iteration 49, residual = 1.1860668787092786e-06
CG iteration 50, residual = 9.384364837569982e-07
CG iteration 51, residual = 7.855316166902487e-07
CG iteration 52, residual = 6.51496622295436e-07
CG iteration 53, residual = 5.847843124222842e-07
CG iteration 54, residual = 5.642748143010168e-07
CG iteration 55, residual = 4.856169352654841e-07
CG iteration 56, residual = 3.649036054484456e-07
CG iteration 57, residual = 2.8732276253074997e-07
CG iteration 58, residual = 2.524271052094127e-07
CG iteration 59, residual = 2.1120183910234245e-07
CG iteration 60, residual = 1.8157945371824184e-07
CG iteration 61, residual = 1.6765792567393462e-07
CG iteration 62, residual = 1.3534309873823607e-07
CG iteration 63, residual = 1.074062546095508e-07
CG iteration 64, residual = 8.692499337660179e-08
CG iteration 65, residual = 6.991024642038307e-08
CG iteration 66, residual = 6.166820848559601e-08
CG iteration 67, residual = 5.426467057609458e-08
CG iteration 68, residual = 4.49261663046699e-08
CG iteration 69, residual = 3.427094557093552e-08
CG iteration 70, residual = 2.736795235873215e-08
CG iteration 71, residual = 2.2107937585505005e-08
CG iteration 72, residual = 1.8685912951579247e-08
CG iteration 73, residual = 1.731690214853151e-08
CG iteration 74, residual = 1.5508098318228793e-08
CG iteration 75, residual = 1.3238529365862859e-08
CG iteration 76, residual = 9.994763302404991e-09
CG iteration 77, residual = 7.883313340279854e-09
CG iteration 78, residual = 6.787391707677259e-09
CG iteration 79, residual = 6.238631289862179e-09
CG iteration 80, residual = 5.761549942545106e-09
CG iteration 81, residual = 4.886605168416044e-09
CG iteration 82, residual = 3.748601507132315e-09
CG iteration 83, residual = 2.7484507090394886e-09
CG iteration 84, residual = 2.280167900036893e-09
CG iteration 85, residual = 2.022692408720981e-09
CG iteration 86, residual = 1.8702256449322423e-09
CG iteration 87, residual = 1.5609299345558527e-09
CG iteration 88, residual = 1.2269782737714562e-09
CG iteration 89, residual = 9.112899530884763e-10
CG iteration 90, residual = 7.127246944419338e-10
CG iteration 91, residual = 5.937505275917352e-10
CG iteration 92, residual = 5.514127182356387e-10
CG iteration 93, residual = 4.998602007652963e-10
CG iteration 94, residual = 4.123478055496168e-10
CG iteration 95, residual = 3.2658139862968133e-10
CG iteration 96, residual = 2.597210990932084e-10
CG iteration 97, residual = 2.1772981031330537e-10
CG iteration 98, residual = 2.00538955309345e-10
CG iteration 99, residual = 1.86415938511895e-10
CG iteration 100, residual = 1.6250867679783661e-10
CG iteration 101, residual = 1.2830147678396147e-10
CG iteration 102, residual = 9.968529926059654e-11
CG iteration 103, residual = 7.990060601783541e-11
CG iteration 104, residual = 7.088942993466392e-11
CG iteration 105, residual = 6.66505875845156e-11
CG iteration 106, residual = 5.949849939096571e-11
CG iteration 107, residual = 4.792258582008747e-11
CG iteration 108, residual = 3.8393227058244564e-11
CG iteration 109, residual = 2.982716118376666e-11
CG iteration 110, residual = 2.524716036888484e-11
CG iteration 111, residual = 2.3865545508398605e-11
CG iteration 112, residual = 2.2847911971004767e-11
CG iteration 113, residual = 2.00474497637047e-11
CG iteration 114, residual = 1.5427221417149875e-11
CG iteration 115, residual = 1.217123837294711e-11
CG iteration 116, residual = 1.024274051146575e-11
CG iteration 117, residual = 1.0046368766212752e-11
CG iteration 118, residual = 9.287213437759128e-12
CG iteration 119, residual = 8.519338152489992e-12
CG iteration 120, residual = 7.044661640421685e-12
CG iteration 121, residual = 5.372879352132866e-12
CG iteration 122, residual = 4.213435238217594e-12
CG iteration 123, residual = 3.8401466277157895e-12
CG iteration 124, residual = 3.62415267088093e-12
CG iteration 125, residual = 3.0690688642693197e-12
CG iteration 126, residual = 2.462572658744305e-12
CG iteration 127, residual = 1.8937939799233936e-12
CG iteration 128, residual = 1.5445352558967003e-12
CG iteration 129, residual = 1.3365937485173723e-12
CG iteration 130, residual = 1.2596992284315248e-12
CG iteration 131, residual = 1.1246386318521103e-12
CG iteration 132, residual = 9.044199008153616e-13
CG iteration 133, residual = 6.755353669204546e-13
CG iteration 134, residual = 5.478309832949945e-13
CG iteration 135, residual = 4.587901541843361e-13
CG iteration 136, residual = 4.207573254604881e-13
CG iteration 137, residual = 3.8906949046626835e-13
CG iteration 138, residual = 3.4572985342329676e-13
CG iteration 139, residual = 2.659787680982204e-13
CG iteration 140, residual = 2.111743198993406e-13

[12]:

BaseWebGuiScene

[ ]:

[ ]:

[ ]: