Symbolic definition of forms : magnetic field

We compute the magnetic field generated by a coil placed on a C-core. We see how to

• model a 3D constructive solid geometry

• set material properties from domain and boundary labels

• define bilinear- and linear forms symbolically using trial- and testfunctions

Download cmagnet.py

from netgen.csg import *
from ngsolve import *


def MakeGeometry():
    geometry = CSGeometry()
    box = OrthoBrick(Pnt(-1,-1,-1),Pnt(2,1,2)).bc("outer")

    core = OrthoBrick(Pnt(0,-0.05,0),Pnt(0.8,0.05,1))- \
           OrthoBrick(Pnt(0.1,-1,0.1),Pnt(0.7,1,0.9))- \
           OrthoBrick(Pnt(0.5,-1,0.4),Pnt(1,1,0.6)).maxh(0.2).mat("core")
    
    coil = (Cylinder(Pnt(0.05,0,0), Pnt(0.05,0,1), 0.3) - \
            Cylinder(Pnt(0.05,0,0), Pnt(0.05,0,1), 0.15)) * \
            OrthoBrick (Pnt(-1,-1,0.3),Pnt(1,1,0.7)).maxh(0.2).mat("coil")
    
    geometry.Add ((box-core-coil).mat("air"))
    geometry.Add (core)
    geometry.Add (coil)
    return geometry



ngmesh = MakeGeometry().GenerateMesh(maxh=0.5)
ngmesh.Save("coil.vol")
mesh = Mesh(ngmesh)

# curve elements for geometry approximation
mesh.Curve(5)

ngsglobals.msg_level = 5

fes = HCurl(mesh, order=4, dirichlet="outer", nograds = True)

# u and v refer to trial and test-functions in the definition of forms below
u = fes.TrialFunction()
v = fes.TestFunction()

mur = mesh.MaterialCF({ "core" : 1000 }, default=1)
mu0 = 1.257e-6
nu = 1/(mu0*mur)

a = BilinearForm(fes, symmetric=True)
a += nu*curl(u)*curl(v)*dx + 1e-6*nu*u*v*dx

c = Preconditioner(a, type="bddc")
# c = Preconditioner(a, type="multigrid", flags = { "smoother" : "block" } )

f = LinearForm(fes)
f += CoefficientFunction((y,0.05-x,0)) * v * dx("coil")

u = GridFunction(fes)


with TaskManager():
    a.Assemble()
    f.Assemble()
    solver = CGSolver(mat=a.mat, pre=c.mat)
    u.vec.data = solver * f.vec


Draw (u.Deriv(), mesh, "B-field", draw_surf=False)

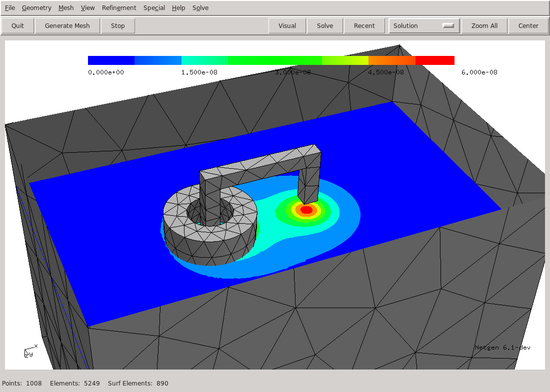
Mesh and magnitude of magnetic field visualized in Netgen: