This page was generated from unit-8.8-aggregation/aggregation.ipynb.

8.8 Cell and basis aggregation in ngsxfem

This unit gives a basic introduction to basis aggregation in ngsxfem. Especially, we treat:

• definition of aggregation patches

• extension of basis functions on aggregation patches

from ngsolve import *
from xfem import *
from ngsolve.webgui import *

importing ngsxfem-2.1.2303.dev0

Introduction: Cut cells' best friends: their neighbors

Let’s start with a simple example (structured mesh, planar domain boundary):

from ngsolve.meshes import MakeStructured2DMesh
mesh = MakeStructured2DMesh(quads=False, nx=3, ny=2)
levelset = x - 0.8
gflset = GridFunction(H1(mesh))
InterpolateToP1(levelset, gflset)
DrawDC(gflset, -1.0, 2.0, mesh, "x")

BaseWebGuiScene

In this simple configuration we have the right block of elements cut by the zero level set.

The cut configuration on cut elements can become arbitrarily bad so that basis functions on the cut elements may have degenerated support

• \(\leadsto\) can lead to stability or (at least) conditioning issues.

To stabilize those cases we often seek for help in the neighborhood. This is typically done either

• through ghost penalty stabilization where essentially functions are glued together weakly in a neighborhood or

• by gluing basis functions on cut elements to basis functions on uncut elements in the virtue of an extrapolation

Patches

To define proper neighborhood regions where support is given from "good" to "bad" elements, we will define patches. First, we will need to define: * which elements are "good" and can serve as "root" elements * and which elements are "bad" and need support. Here, we will make the simple distinction:

\[\text{uncut element} = \text{ "good" element }, \qquad \text{cut element} = \text{ "bad" element }\]

ci = CutInfo(mesh, gflset)
roots = ci.GetElementsOfType(NEG)
bads = ci.GetElementsOfType(IF)
print("bad element array: ", bads)
print("bad elements: ", [i for i in range(len(bads)) if bads[i]])
Draw(BitArrayCF(bads), mesh, "bad_elements")

bad element array:  0: 000011000011
bad elements:  [4, 5, 10, 11]

BaseWebGuiScene

ElementAggregation

Next, we introduce a new class ElementAggregation that organizes the 'neighborhood support':

Let’s have a brief look at its functionality:

help(ElementAggregation)

Help on class ElementAggregation in module xfem.xfem:

class ElementAggregation(pybind11_builtins.pybind11_object)
 |  ElementAggregation does the following:
 |    It collects patches of elements that allow to stabilize bad cut elements by at least one
 |    good element (the root element).
 |  )
 |
 |  Method resolution order:
 |      ElementAggregation
 |      pybind11_builtins.pybind11_object
 |      builtins.object
 |
 |  Methods defined here:
 |
 |  Update(...)
 |      Update(self: xfem.xfem.ElementAggregation, root_elements: pyngcore.pyngcore.BitArray, bad_elements: pyngcore.pyngcore.BitArray, heapsize: int = 1000000) -> None
 |
 |
 |      Updates a Element Aggregation based ...
 |
 |  __init__(...)
 |      __init__(self: xfem.xfem.ElementAggregation, mesh: ngsolve.comp.Mesh, root_elements: object = None, bad_elements: object = None, heapsize: int = 1000000) -> None
 |
 |
 |      Creates a ElementAggregation based on a mesh, a list of root and a list of bad elements.
 |
 |  ----------------------------------------------------------------------
 |  Readonly properties defined here:
 |
 |  element_to_patch
 |      vector mapping elements to (non-trivial) patches
 |
 |  els_in_nontrivial_patch
 |      BitArray that is true for every element that is part of a (non-trivial) patch
 |
 |  els_in_trivial_patch
 |      BitArray that is true for every element that is not part of a (non-trivial) patch
 |
 |  facet_to_patch
 |      vector mapping facets to (non-trivial) patches
 |
 |  patch_interior_facets
 |      BitArray that is true for every facet that is *inside* an aggregation cluster
 |
 |  ----------------------------------------------------------------------
 |  Static methods inherited from pybind11_builtins.pybind11_object:
 |
 |  __new__(*args, **kwargs) from pybind11_builtins.pybind11_type
 |      Create and return a new object.  See help(type) for accurate signature.

Let’s create an ElementAggregation object and obtain a set of patches:

EA = ElementAggregation(mesh, roots, bads)
patch_number_field = GridFunction(L2(mesh))
patch_number_field.vec.FV()[:] = EA.element_to_patch
Draw(patch_number_field, mesh, "patch_number_field", deformation=CF((0,0,0.02*patch_number_field)))

BaseWebGuiScene

Obviously not all elements are in patches. Indeed the root elements that are not involved in supporting a bad element form "trivial patches":

print("trivial root elements:", EA.els_in_trivial_patch)
print("nontrivial elements:", EA.els_in_nontrivial_patch)

trivial root elements: 0: 111000111000
nontrivial elements: 0: 000111000111

Similarly we can also relate facets that lie within a patch to the corresponding patch:

print("EA.patch_interior_facets: ", EA.patch_interior_facets)
print("EA.facet_to_patch: ", EA.facet_to_patch)

EA.patch_interior_facets:  0: 00000001100000000110000
EA.facet_to_patch:  [-1, -1, -1, -1, -1, -1, -1, 0, 0, -1, -1, -1, -1, -1, -1, -1, -1, 1, 1, -1, -1, -1, -1]

So, now we have some nice patches. These can be used to tune ghost penalty terms (reduce the number of facets where GP is applied) or to change the FEM basis which we will discuss next.

Basis aggregation

On each of the patches we now want to get rid of the basis functions that are not supported on "root" elements. Let

\[u(x) = \sum_{i} c_i \varphi_i(x)\]

be your usual development in your basis \(\{\varphi\}_i\). Now, we distinguish \(\mathcal{I}_{\text{root}}\) and \(\mathcal{I}_{\text{bad}}\), the index sets of basis functions with/without support on root elements. Then, for \(i \in \mathcal{I}_{\text{bad}}\) we want to express \(c_i\) as a (linear) function of \((c_j)_{j \in \mathcal{I}_{\text{root}}}\):

We start with

\[u(x) = \sum_{i \in \mathcal{I}_{\text{root}}} c_i \varphi_i(x) + \sum_{i \in \mathcal{I}_{\text{bad}}} c_i \varphi_i(x)\]

and obtain

\[u(x) = \sum_{i \in \mathcal{I}_{\text{root}}} c_i \varphi_i(x) + \sum_{i \in \mathcal{I}_{\text{bad}}} \sum_{c_i \in \mathcal{I}_{\text{root}}} X_{ji} c_j \varphi_i(x) = \sum_{c_i \in \mathcal{I}_{\text{root}}} c_i \underbrace{\sum_{j} E_{ij} \varphi_j(x)}_{\psi_i(x)}\]

Here \(\{\psi_i\}_{i \in \mathcal{I}_{\text{root}}}\) is the new basis obtained after aggregation. We will however characterize it always through the embedding matrix \(E\).

This can now be achieved by the method AggEmbedding which yields the embedding matrix \(E\) (we explain how \(E\) is obtained below).

help(AggEmbedding)

Help on function AggEmbedding in module xfem:

AggEmbedding(EA, fes, deformation=None, heapsize=1000000)
    Computes and returns embedding matrix for a patchwise polynomial extension
    (realized through ghost penalties),
    followed by averaging if some dofs are shared by multiple patches.

    Parameters

    elagg : ElementAggregation
      ElementAggregation instace defining the patches which are aggregated into a single element

    fes : ngsolve.FESpace
      The finite element space which is aggregated.

    deformation : ngsolve.GridFunction [mesh.dim]
      The mesh deformation (needed for Ghost penalty assembly)

    heapsize : int
        heapsize for local computations.

L2 low order

Let us try it out for the space of piecewise constants first:

fes = L2(mesh, order=0)
E = AggEmbedding(EA, fes)
from helper import ShowPattern
ShowPattern(E)
print(E)

/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.4
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

Row 0:   0: 1
Row 1:   1: 1
Row 2:   2: 1
Row 3:   3: 1
Row 4:   3: 1
Row 5:   3: 1
Row 6:   4: 1
Row 7:   5: 1
Row 8:   6: 1
Row 9:   7: 1
Row 10:   7: 1
Row 11:   7: 1

Let us take a look at the basis functions:

def ExtendedBasisFunctionsAsMultiDim(EA, fes):
    E = AggEmbedding(EA, fes)
    gfshow = GridFunction(fes, multidim=0)
    gf = GridFunction(fes)
    coefvec = E.CreateRowVector()
    for i in range(E.width):
        coefvec[:] = 0
        coefvec[i] = 1
        gf.vec.data = E * coefvec
        gfshow.AddMultiDimComponent(gf.vec)
    return gfshow

gfshow = ExtendedBasisFunctionsAsMultiDim(EA,fes)
Draw (gfshow, mesh, interpolate_multidim=False, animate=False, autoscale=True);

Use the multidim-slider in the webgui to change the (interior) basis function and see the extended basis functions.

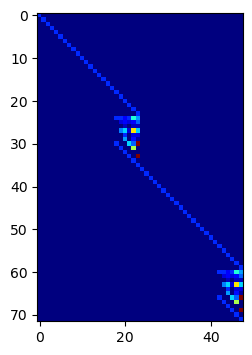
L2 higher order

Now, higher order:

fes = L2(mesh, order=2)
ShowPattern(AggEmbedding(EA, fes))
gfshow = ExtendedBasisFunctionsAsMultiDim(EA,fes)
Draw (gfshow, mesh, interpolate_multidim=False, animate=False, autoscale=True);

H1

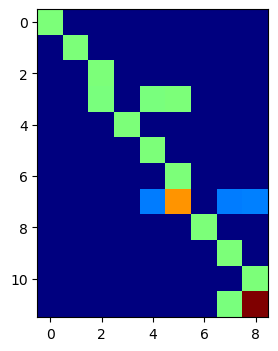
When considering spaces with (partial) continuity, some dofs may appear in several patches but not on a root element. In this case the extensions are average:

fes = H1(mesh, order=1)
ShowPattern(AggEmbedding(EA, fes))
gfshow = ExtendedBasisFunctionsAsMultiDim(EA,fes)
Draw (gfshow, mesh, interpolate_multidim=False, animate=False, autoscale=True);

Vector-valued spaces

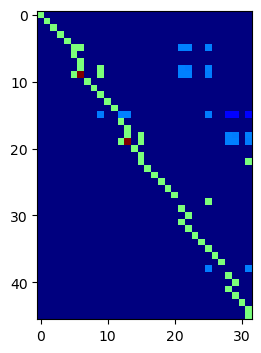
And now, HDiv

fes = HDiv(mesh, order=1)
ShowPattern(AggEmbedding(EA, fes))
gfshow = ExtendedBasisFunctionsAsMultiDim(EA,fes)
Draw (gfshow, mesh, interpolate_multidim=False, animate=False, autoscale=True);

How it works

The mechanism behind the patchwise extension is very generic and obviously works for L2, H1, HDiv, … in a generic way. But how?

A formulation as a harmonic extension

Let \(w_h(x) = \sum_{i \in \mathcal{I}_{\text{bad}}} c_i \varphi_i(x)\) be a finite element function only supported on bad elements and \(W_h\) the corresponding subspace of the underlying FE space \(V_h\) and \(X_h = W_h \setminus V_h\).

The idea is now that for every basis function \(\varphi_i\) with \(i \in \mathcal{I}_{\text{root}}\) we define its extension into \(W_h\) through

\[\operatorname{argmin}_{w_h \in W_h} \vert \varphi_i + w_h \vert_\ast\]

where \(\vert \cdot \vert_\ast\) is a smoothness-measuring semi-norm. \(w_h\) is like a harmonic extension from the "root" into the "bad" elements.

A formulation as a patch-wise harmonic extension

To localize this problem we proceed patch-by-patch:

For every patch \(\omega\) we define \(W_h^{\omega}\) through functions that are supported on the patch, but not on a root element. Note that some basis function may appear in different patches now.

Then, we solve the local patch problems: For every basis function \(\varphi_i\) with \(i \in \mathcal{I}_{\text{root}}\) and support on the patch \(\omega\) we define its extension into \(W_h^\omega\) through

\[\operatorname{argmin}_{w_h \in W_h^\omega} \vert \varphi_i + w_h \vert_{\ast,\omega}\]

where \(\vert \cdot \vert_{\ast,\omega}\) is a smoothness-measuring semi-norm.

The thusly obtained extended functions are afterwards averaged.

A generic semi-norm \(\vert \varphi_i + w_h \vert_{\ast,\omega}\)

It now remains to define a proper semi-norm.

When using AggEmbedding as above the chosen semi-norm is defined through a ghost penalty term inside all patches (Note that patch-wise polynomials form the kernel of that operator):

def AggEmbedding(EA, fes, deformation=None, heapsize=1000000):
    """..."""
    u,v = fes.TnT()
    ghost_penalty = (u - u.Other()) * (v - v.Other()) * dFacetPatch(deformation=deformation)
    return ExtensionEmbedding(EA, fes, ghost_penalty, heapsize=heapsize)

If you want to use a different semi-norm for the extension, you can use ExtensionEmbedding accordingly.

Applications of patch aggregations

We now have learned about how to form patches and extend basis functions. This can be exploited in several ways:

1. To solve CutFEM problems where the resulting system is reduced to the root unknowns by the embedding, cf. the fictdom_aggfem.py demo of ngsxfem.

2. Patches can be used to minimize the facets that are used in ghost penalty stabilizations, cf. e.g. unfmixed example.

3. Patches can be used to solve local patch-wise problems, e.g. for postprocessings in unfitted mixed methods, cf. unfmixed example.