This page was generated from unit-8.6-mlset_basic/mlset_basic.ipynb.

8.6 Integration over domains described by multiple level sets

The ngsxfem add-on library has the ability to integrate over domains which are defined by muliple level set functions.

We recall that previously, our domain of interest was described by a single level set function, i.e., for a continuous level set function \(\phi\), we considered the domain \(\Omega_{-} := \{x : \phi(x) < 0 \}\).

Now, let us consider the set \(\{\phi_i \}\) of level set functions. With this we define the domain of interest by the intersection \(\Omega := \bigcap_i \{\phi_i < 0\}\).

The libraries are imported as usual:

# Import geometry features, NGSolve and xfem
from netgen.geom2d import SplineGeometry
from ngsolve import *
from xfem import *

# Visualisation
from ngsolve.webgui import *
DrawDC = MakeDiscontinuousDraw(Draw)

importing ngsxfem-2.1.2405.dev0

For a better interactive experience set the following parameter to 2 (1 leads to coarse grids). It is set to 1 for the documentation to keep file sizes at a managable level:

interactive = 1

We generate a background mesh

geo = SplineGeometry()
geo.AddRectangle([-1, -0.5], [1, 1.5], bc=1)
mesh = Mesh (geo.GenerateMesh(maxh=0.3, quad_dominated=False))
Draw(mesh, 0, 0)

BaseWebGuiScene

Integrating over regions of co-dimension 0

As an example, we shall consider an isosceles triangle, described by the level set functions \(\phi_1 = y - 1\), \(\phi_2 = 2x - y\) and \(\phi_3 = -2x - y\).

As in the single level set setting, ngsxfem can only handle piecewise linear level set functions. We thefore interpolate each smooth level set into an P1 GridFunction \(\phi^\ast_i \in \mathcal{P}^1(T), T \subset \Omega\). In order to use these more easily later on, we store them in a tuple.

level_sets = (y-1, 2*x-y, -2*x-y)
nr_ls = len(level_sets)
level_sets_p1 = tuple(GridFunction(H1(mesh, order=1)) for i in range(nr_ls))

for i, lset_p1 in enumerate(level_sets_p1):
    InterpolateToP1(level_sets[i], lset_p1)
    DrawDC(lset_p1, -3.5, 2.5, mesh, "lset_p1_{}".format(i))

The domain described where all three level-sets are negavive is then

Draw(CoefficientFunction((level_sets_p1[0], level_sets_p1[1], level_sets_p1[2], 0)),
     mesh, "NEG-NEG-NEG", min=-1, max=1,
     eval_function="value.x<0.0?(value.y<0.0?(value.z<0.0?1.0:-1.0):-1.0):-1.0")

BaseWebGuiScene

To integrate, we still use the function Integrate. In the multiple level set context, the input to the dCut(levelset, domain_type, order) is very similar to the single level set setting. Here, * the levelset argument must be a tuple of the P1-GridFunction level set functions and * the domain_type can be a * tuple({NEG, POS, IF}) of the same length as the levelset tuple which describes the domain whith respect each level set function * list(tuple) of such tuples when the domain is described via (the union of) multiple regions * DomainTypeArray (see xfem.mlset convininece layer below). * the remaining (keyword) arguments remain as in the single level set case

area = Integrate(CoefficientFunction(1) * dCut(level_sets_p1, (NEG, NEG, NEG), order=0), mesh=mesh)
error = abs(area - 0.5)
print("Result of the integration: {}".format(area))
print("Error of the integration: {:5.3e}".format(error))

Result of the integration: 0.5
Error of the integration: 0.000e+00

Since the smooth level set functions are linear, the integration is exact up to mashine precision.

Integrating over regions of co-dimension > 0

We can also integrate over subdomains of higher codimensions. For example, the lenghths of the sides of the triangle can be computed as follows:

len_top = Integrate(CoefficientFunction(1) * dCut(level_sets_p1, (IF, NEG, NEG), order=0), mesh)
print("Top side-length of the triangle");
print("Result of the integration: {}".format(len_top))
print("Error of the integration: {:5.3e}".format(abs(len_top - 1)))

len_right = Integrate(CoefficientFunction(1) * dCut(level_sets_p1, (NEG, IF, NEG), order=0), mesh)
print("\nRight side-length of the triangle")
print("Result of the integration: {}".format(len_right))
print("Error of the integration: {:5.3e}".format(abs(len_right - sqrt(5)/2)))

len_left = Integrate(CoefficientFunction(1) * dCut(level_sets_p1, (NEG, NEG, IF), order=0), mesh)
print("\nLeft side-length of the triangle")
print("Result of the integration: {}".format(len_left))
print("Error of the integration: {:5.3e}".format(abs(len_left - sqrt(5)/2)))

Top side-length of the triangle
Result of the integration: 1.0
Error of the integration: 0.000e+00

Right side-length of the triangle
Result of the integration: 1.1180339887498945
Error of the integration: 4.441e-16

Left side-length of the triangle
Result of the integration: 1.1180339887498947
Error of the integration: 2.220e-16

To compute the perimeter of the triangle, we can pass a list containing the tuples describing each side to Integrate via the domain_type entry in the levelset_domain dictionary:

domain_list = [(IF, NEG, NEG), (NEG, IF, NEG), (NEG, NEG, IF)]
len_together =  Integrate(CoefficientFunction(1) * dCut(level_sets_p1, domain_list, order=0), mesh)


print("Perimeter of the triangle")
print("Result of the integration: {}".format(len_together))
print("Error of the integration: {:5.3e}".format(abs(len_together - 1 - sqrt(5))))

Perimeter of the triangle
Result of the integration: 3.2360679774997894
Error of the integration: 4.441e-16

Similarly, we can also perform point evaluations at (codim 2) intersections of level sets:

point_val = Integrate((x**2 + y**2) * dCut(level_sets_p1, (IF, IF, NEG), order=0), mesh)

print("Result of the integration: {}".format(point_val))
print("Error of the integration: {:5.3e}".format(abs(point_val - 1.25)))

Result of the integration: 1.25
Error of the integration: 0.000e+00

Convenience Layer: xfem.mlset

In order to work with more complex domains, described by multiple level sets, we provide a convenience layer in the module xfem.mlset. At its core, this module provides a container class DomainTypeArray which allows us to perform operations and manipulate domain regions. A full description of this can be cound in the docstring:

from xfem.mlset import *

DomainTypeArray?

Working with DomainTypeArrays

A DomainTypeArray is initialised either with a tuple({NEG,POS,IF,ANY}) or with a list of such tuples. While integration does not work with COMBINED_DOMAIN_TYPES, the DomainTypeArray class accepts ANY as an entry, and expands this internaly to a list of tuples containing only {IF, POS, NEG}, such that the result can then be used for integration.

domain = DomainTypeArray((ANY, NEG, POS))

The list of regions contained in this can then be acessed via the as_list attribute

domain.as_list

[(<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>)]

and the codimension of the resulting domain can be accesed via the codim attribute

domain.codim

0

Geometrical features

The main feature of the DomainTypeArray class is that we can treat it as a geometrical set and thus can perform logical operations with them. Available operators are:

Operator	Operation	Remark
~	Returns a DomainTypeArray describing the region NOT part of the original region.	The result keeps the codimension.
\|	Returns a DomainTypeArray describing the region defined by the UNION of two regions.	Only possible for domains of the same codimension.
&	Returns a DomainTypeArray describing the region defined by the INTERSECTION of two regions.	Intersections can increase the codimension.

Note: - For | and &, the tuples in each DomainTypeArray must have the same length. - The operators &= and |= are also available.

triangle = DomainTypeArray((NEG,NEG,NEG))
outside_triangle = ~triangle
outside_triangle.as_list

[(<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>)]

dta1 = DomainTypeArray((POS, NEG)) | DomainTypeArray([(POS,POS),(NEG,POS)])
dta1.as_list

[(<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>)]

dta2 = outside_triangle & DomainTypeArray([(POS, NEG, POS), (POS, POS, POS)])
dta2.as_list

[(<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>)]

dta3 = DomainTypeArray((NEG, IF, POS)) & DomainTypeArray((NEG, POS, IF))
dta3.as_list

[(<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.IF: 2>)]

Generating the boundary

In order to obtain the boundary of the region described by a DomainTypeArray we can use the class .Boundary() method:

boundary = triangle.Boundary()
boundary.as_list

[(<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.IF: 2>),
 (<DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>)]

Since each section in a DomainTypeArray is considered as a separate domain, we can even go one step further and construct the corners:

corners = boundary.Boundary()
corners.as_list

[(<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.IF: 2>),
 (<DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.IF: 2>),
 (<DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.IF: 2>, <DOMAIN_TYPE.NEG: 0>)]

Visualisation Tools

To help visualise the regions descibed by a DomainTypeArray for debugging purposes, we can use the .Indicator(lsets) method for domains of codim=0 and the IndicatorSmoothed(lsets, eps=0.03) method for domains of codim>0.

These functions return a CoefficientFunction which has the value 1 inside the region of interest and is 0 elsewhere. For regions of co-dimension>0, the result of IndicatorSmoothed(lsets, eps) is a CoefficientFunction with the value 1 in the eps region around the domain.

For illustration purposes, we shall consider fine meshes here, in order to render the indicator functions accurately within the NGSolve webgui. Alternaltievly, it is possible to visualise the indicator functions on coarse meshes in the netgen gui or in paraview (using vtk outputs). In these cases, a larger number of subdivisions is then necessary to get a resonalbly sharp representation on elements with multiple cuts.

if interactive > 1:
    nref = 4
else:
    nref = 2
for i in range(nref):
    mesh.ngmesh.Refine()
mesh=Mesh(mesh.ngmesh)

for i, lset_p1 in enumerate(level_sets_p1):
    lset_p1.Update()
    InterpolateToP1(level_sets[i], lset_p1)

DrawDC(outside_triangle.Indicator(level_sets_p1), -3.5, 2.5, mesh, "outside_indicator")

BaseWebGuiScene

Similarly, DomainTypeArray.IndicatorSmoothed(level_sets, eps) returns a CoefficientFunction which has the value 1 in the eps-strip around the interface described in DomainTypeArray. This assumes that each level set function is approximately a distance function around the interface:

DrawDC(boundary.IndicatorSmoothed(level_sets_p1, 0.05/interactive), -3.5, 2.5, mesh,
       "boundary_indicator")

BaseWebGuiScene

DrawDC(corners.IndicatorSmoothed(level_sets_p1, 0.06/interactive), -3.5, 2.5, mesh, "boundary_indicator")

BaseWebGuiScene

Removing unnecesary regions

These operations take place on a pure logical DOMAIN_TYPE level, without taking ang geometrical information into account.

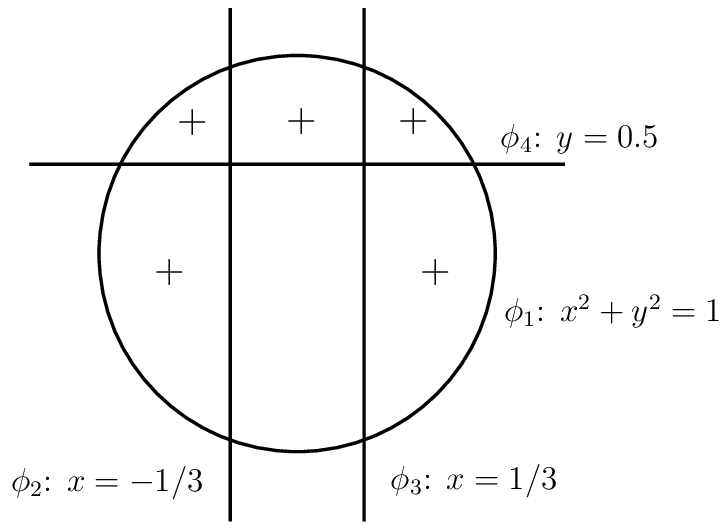
Let us again consider the above case of a Zalesak Disk consisting of the 5 regions, marked with a \(+\): "

"

geo = SplineGeometry()
geo.AddRectangle((-1.1, -1.1), (1.1, 1.1), bc=1)
mesh = Mesh(geo.GenerateMesh(maxh=0.2/interactive))

level_sets = [x * x + y * y - 1, -x - 1 / 3, x - 1 / 3, y - 0.5]
level_sets_p1 = tuple(GridFunction(H1(mesh, order=1))
                      for i in range(len(level_sets)))

for i, lsetp1 in enumerate(level_sets_p1):
    InterpolateToP1(level_sets[i], lsetp1)
    DrawDC(lsetp1, -3.5, 2.5, mesh, "lset_p1_" + str(i))

The easiest way to generate this is to use the DomainTypeArray functionality:

z_disc =    DomainTypeArray((NEG,ANY,ANY,ANY)) \
         & ~DomainTypeArray((NEG,NEG,NEG,NEG))
z_disc.as_list

[(<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>)]

DrawDC(z_disc.Indicator(level_sets_p1), -3.5, 2.5, mesh, "zdisc")

BaseWebGuiScene

However, we note that there are 7 regions, rather than the expected 5. However, on closer inspection, we see that (NEG, POS, POS, POS) and (NEG, POS, POS, NEG) are regions that do not exist with respect to our level sets.

We have two options to remove such irrelevant regions from a DomainTypeArray:

First:

If the object has already been created, we can use the .Compress(lsets, persistent=False) method. Given a tuple of level set functions lsets, the .Compress method removes any domain tuples from the instance, which have zero measure with respect to these level set functions. If persistent=True is passed to .Compress, then any DomainTypeArrays derived from the compressed one will also be compressed with respect to the here given set of level set fucntions.

So that we are able to integrate internally, lsets needs to be of the type tuple(ngsolve.GridFunction), such that we have acess to the mesh.

z_disc.as_list

[(<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>)]

z_disc.Compress(level_sets_p1)
z_disc.as_list

[(<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>)]

This removes the unnecessary regions (NEG, POS, POS, POS) and (NEG, POS, POS, NEG).

Second:

On initialisation of a DomainTypeArray, we can also pass a tuple lsets of level sets for compression at initilisation, and a flag persistent_compress which indicates, whether the result when using operators schould again be compressed with respect to the same set of level sets

tmp1 = DomainTypeArray((NEG,ANY,ANY,ANY),
                       lsets=level_sets_p1,
                       persistent_compress=True)
tmp2 = DomainTypeArray((NEG,NEG,NEG,NEG),
                       lsets=level_sets_p1,
                       persistent_compress=True)
z_disc2 = tmp1 & ~tmp2
z_disc2.as_list

[(<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>)]

The difference between persistent_compress=True/False becomes more apparent when computing the boundary.

z_disc = DomainTypeArray((NEG,ANY,ANY,ANY)) & ~DomainTypeArray((NEG,NEG,NEG,NEG))
bnd1 = z_disc.Boundary()
DrawDC(bnd1.IndicatorSmoothed(level_sets_p1,0.08/interactive), -3.5, 2.5, mesh, "bnd1")
bnd1.as_list

[(<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>)]

bnd2 = z_disc2.Boundary()
DrawDC(bnd2.IndicatorSmoothed(level_sets_p1,0.08/interactive), -3.5, 2.5, mesh, "bnd2")
bnd2.as_list

[(<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>),
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>),
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>)]

Generating outward pointing unit normal vectors

To implement boundary conditions using Nitsche’s method, for example in a CutFEM problem, the outward pointing unit normal vectors are needed. Since in the multiple level set setting the boundary can consist of many sections (8 in the case of the Zalesak disk), we have a member function to compute the outward pointing unit normal vector on each section of the boundary of a codim=0 domain.

normals = z_disc2.GetOuterNormals(level_sets_p1)
normals

{(<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>): <ngsolve.fem.CoefficientFunction at 0x7f10ac110d70>,
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>): <ngsolve.fem.CoefficientFunction at 0x7f10ac110bf0>,
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>): <ngsolve.fem.CoefficientFunction at 0x7f10ac110e30>,
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>): <ngsolve.fem.CoefficientFunction at 0x7f10ac110890>,
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>): <ngsolve.fem.CoefficientFunction at 0x7f10ac110710>,
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>): <ngsolve.fem.CoefficientFunction at 0x7f10ac111d30>,
 (<DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.NEG: 0>): <ngsolve.fem.CoefficientFunction at 0x7f10ac1124b0>,
 (<DOMAIN_TYPE.IF: 2>,
  <DOMAIN_TYPE.NEG: 0>,
  <DOMAIN_TYPE.POS: 1>,
  <DOMAIN_TYPE.POS: 1>): <ngsolve.fem.CoefficientFunction at 0x7f10ac1137d0>}

ngsolve.internal.visoptions.showsurfacesolution=1
Draw(normals[(IF,NEG,NEG,POS)], mesh, "normal_1", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((IF,NEG,NEG,POS)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5, mesh, "boundary_1")

BaseWebGuiScene

Draw(normals[(NEG,NEG,NEG,IF)], mesh, "normal_2", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((NEG,NEG,NEG,IF)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_2")

BaseWebGuiScene

Draw(normals[(IF,NEG,POS,NEG)], mesh, "normal_3", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((IF,NEG,POS,NEG)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_3")

BaseWebGuiScene

Draw(normals[(NEG,NEG,IF,NEG)], mesh, "normal_4", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((NEG,NEG,IF,NEG)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_4")

BaseWebGuiScene

Draw(normals[(IF,POS,NEG,POS)], mesh, "normal_5", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((IF,POS,NEG,POS)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_5")

BaseWebGuiScene

Draw(normals[(IF,POS,NEG,NEG)], mesh, "normal_6", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((IF,POS,NEG,NEG)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_6")

BaseWebGuiScene

Draw(normals[(NEG,IF,NEG,NEG)], mesh, "normal_7", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((NEG,IF,NEG,NEG)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_7")

BaseWebGuiScene

Draw(normals[(IF,NEG,POS,POS)], mesh, "normal_8", vectors={'grid_size': 14})
DrawDC(DomainTypeArray((IF,NEG,POS,POS)).IndicatorSmoothed(level_sets_p1, eps=0.08/interactive), -3.5, 2.5,  mesh, "boundary_8")

BaseWebGuiScene

Integrating using DomainTypeArrays

In order to use DomainTypeArrays for integration purposes we can simply pass the DomainTypeArray to the domain_type argumet of the SymbolicDifferentialSymbol dCut:

from math import pi
area_zd = pi - 2 / 3 * (0.5 + sqrt(2) * 2 / 3)
area_zd += - (2 * asin(1 / 3) - sin(2 * asin(1 / 3))) / 2

area = Integrate(CoefficientFunction(1) * dCut(level_sets_p1, z_disc2, order=0), mesh)

print("Area 2 = {:12.10f}".format(area))
print("Error: {:4.2e}".format(abs(area - area_zd)))

Area 2 = 2.1260431413
Error: 2.81e-02

Since the smooth level sets are not all piecewise linear, integration is only accurate up to \(\mathcal{O}(h^2)\)

Constructing new domais from ``DomainTypeArrays`` defined with respect to different level sets

Some complicated gemetries consist of the union or the intersection of geometrical objects which are easily descriped be a small number of level sets. For this purpose xfem.mlset provides the two functions TensorUnion and TensorIntersection, which generate the DomainTypeArray description from the union or intersection of different DomainTypeArrays, each defined with respect to different level sets.

For example, consider the follwoing two triangular domains:

geo = SplineGeometry()
geo.AddRectangle((-2.5, -1), (1, 2.5), bc=1)
mesh = Mesh(geo.GenerateMesh(maxh=0.3/interactive))

level_sets1 = [-2*x + y - 1, 2*x + y - 1, -y + 2]
dta1 = DomainTypeArray((POS, POS, POS))
DrawDC(dta1.Indicator(level_sets1), -3.5, 2.5, mesh, "dta1")

level_sets2 = [-2*x + y - 4, 2*x + y + 2, -y]
dta2 = DomainTypeArray((NEG, NEG, NEG))
DrawDC(dta2.Indicator(level_sets2), -3.5, 2.5, mesh, "dta2")

BaseWebGuiScene

Then we can construct the Union of these two domains as

dta_union = TensorUnion(dta1, dta2)
DrawDC(dta_union.Indicator(level_sets1 + level_sets2), -3.5, 2.5, mesh, "union")

BaseWebGuiScene

Note, that a the same result would have been achieved "by hand" with

dta3 = DomainTypeArray([(POS, POS, POS, ANY, ANY, ANY),
                        (ANY, ANY, ANY, NEG, NEG, NEG)])
DrawDC(dta3.Indicator(level_sets1 + level_sets2), -3.5, 2.5, mesh, "union")

BaseWebGuiScene

Unsing TensorIntersection we can also generate the domain description of "outside both triangles"

dta_outside = TensorIntersection(~dta1, ~dta2)
DrawDC(dta_outside.Indicator(level_sets1 + level_sets2), -3.5, 2.5, mesh, "outside")

BaseWebGuiScene

Notehowever, that the description can be very long and contain non existent regions. This is because the DomainTypeArray does not have any information on the actual level sets used to define the domains.

print(dta_outside)
print("Number of regions in DomainTypeArray:", len(dta_outside))

DomainTypeArray:
  Co-dim : 0
  Domains: [(<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>), (<DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.POS: 1>, <DOMAIN_TYPE.NEG: 0>, <DOMAIN_TYPE.NEG: 0>)]
Number of regions in DomainTypeArray: 49

In such cases, using the .Compress() memeber of DomainTypeArray can make sense, to remove regions which do not contibute to the domain for the given level sets:

P1 = H1(mesh, order=1)
levelsets_p1 = tuple([GridFunction(P1) for _l in level_sets1 + level_sets2])
for lsetp1, lset in zip(levelsets_p1, level_sets1 + level_sets2):
    InterpolateToP1(lset, lsetp1)

dta_outside.Compress(levelsets_p1)
print("Number of regions in DomainTypeArray after compression:", len(dta_outside))

Number of regions in DomainTypeArray after compression: 16

DrawDC(dta_outside.Indicator(levelsets_p1), -3.5, 2.5, mesh, "outside")

BaseWebGuiScene