This page was generated from unit-5.5-cuda/poisson_cuda.ipynb.

5.5.1 Solving the Poisson Equation on devices

• After finite element discretization we obtain a (linear) system of equations.

• The new ngscuda module moves the linear operators to the Cuda - decice.

• The host is stearing, data stays on the device

• The module is now included in NGSolve Linux - distributions, and can be used whenever an accelerator card by NVIDIA is available, and the cuda-runtime is installed.

from ngsolve import *
from ngsolve.webgui import Draw
from time import time

mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
for l in range(5): mesh.Refine()
fes = H1(mesh, order=2, dirichlet=".*")
print ("ndof =", fes.ndof)

u, v = fes.TnT()
with TaskManager():
    a = BilinearForm(grad(u)*grad(v)*dx+u*v*dx).Assemble()
    f = LinearForm(x*v*dx).Assemble()

gfu = GridFunction(fes)

jac = a.mat.CreateSmoother(fes.FreeDofs())

with TaskManager():
    inv_host = CGSolver(a.mat, jac, maxiter=2000)
    ts = time()
    gfu.vec.data = inv_host * f.vec
    te = time()
    print ("steps =", inv_host.GetSteps(), ", time =", te-ts)

# Draw (gfu);

ndof = 472321
steps = 1738 , time = 9.076069116592407

Now we import the NGSolve - cuda library.

It provides

• an UnifiedVector, which allocates memory on both, host and device. The data is updated on demand either on host, or on device.

• NGSolve - matrices can create their counterparts on the device. In the following, the conjugate gradients iteration runs on the host, but all operations involving big data are performed on the accelerator.

try:
    from ngsolve.ngscuda import *
except:
    print ("no CUDA library or device available, using replacement types on host")

ngsglobals.msg_level=1
fdev = f.vec.CreateDeviceVector(copy=True)

no CUDA library or device available, using replacement types on host
No device creator function, creating host vector

adev = a.mat.CreateDeviceMatrix()
jacdev = jac.CreateDeviceMatrix()

inv = CGSolver(adev, jacdev, maxsteps=2000, printrates=False)

ts = time()
res = (inv * fdev).Evaluate()
te = time()

print ("Time on device:", te-ts)
diff = Norm(gfu.vec - res)
print ("diff = ", diff)

Time on device: 29.23507070541382
diff =  0.0

On an A-100 device I got (for 5 levels of refinement, ndof=476417):

Time on device: 0.4084775447845459 diff = 3.406979028373306e-12

CG Solver with Block-Jacobi and exact low-order solver:

\[\begin{split}A = \left( \begin{array}{cc} A_{cc} & A_{cf} \\ A_{fc} & A_{ff} \end{array} \right)\end{split}\]

Additive Schwarz preconditioner:

\[C^{-1} = P A_{cc}^{-1} P^T + \sum_i E_i A_i^{-1} E_i^T\]

with

• \(P\) .. embedding of low-order space

• \(A_i\) .. blocks on edges/faces/cells

• \(E_i\) .. embedding matrices

fes = H1(mesh, order=5, dirichlet=".*")
print ("ndof =", fes.ndof)

u, v = fes.TnT()
with TaskManager():
    a = BilinearForm(grad(u)*grad(v)*dx+u*v*dx).Assemble()
    f = LinearForm(x*v*dx).Assemble()

gfu = GridFunction(fes)

jac = a.mat.CreateBlockSmoother(fes.CreateSmoothingBlocks())
lospace = fes.lospace
loinv = a.loform.mat.Inverse(inverse="sparsecholesky", freedofs=lospace.FreeDofs())
loemb = fes.loembedding

pre = jac + loemb@loinv@loemb.T
print ("mat", a.mat.GetOperatorInfo())
print ("preconditioner:")
print(pre.GetOperatorInfo())

with TaskManager():
    inv = CGSolver(a.mat, pre, maxsteps=2000, printrates=False)
    ts = time()
    gfu.vec.data = inv * f.vec
    te = time()
    print ("iterations =", inv.GetSteps(), "time =", te-ts)

ndof = 2947201
mat SparseMatrixd, h = 2947201, w = 2947201

preconditioner:
SumMatrix, h = 2947201, w = 2947201
  BlockJacobi-d, h = 2947201, w = 2947201
  EmbeddedTransposeMatrix, h = 2947201, w = 2947201
    EmbeddedMatrix, h = 2947201, w = 118401
      SparseCholesky-d, h = 118401, w = 118401

iterations = 37 time = 5.271472930908203

adev = a.mat.CreateDeviceMatrix()
predev = pre.CreateDeviceMatrix()
fdev = f.vec.CreateDeviceVector()

with TaskManager():
    inv = CGSolver(adev, predev, maxsteps=2000, printrates=False)
    ts = time()
    gfu.vec.data = (inv * fdev).Evaluate()
    te = time()
    print ("iterations =", inv.GetSteps(), "time =", te-ts)

No device creator function, creating host vector
iterations = 37 time = 5.498937606811523

on the A-100:

SumMatrix, h = 2896001, w = 2896001 N4ngla20DevBlockJacobiMatrixE, h = 2896001, w = 2896001 EmbeddedTransposeMatrix, h = 2896001, w = 2896001 EmbeddedMatrix, h = 2896001, w = 116353 N4ngla17DevSparseCholeskyE, h = 116353, w = 116353 iterations = 37 time= 0.6766986846923828

Using the BDDC preconditioner:

For the BDDC (balancing domain decomposition with constraints) preconditioning, we build a FEM system with relaxed connectivity:

This allows for static condensation of all local and interface degrees of freedom, only the wirebasket dofs enter the global solver. The resulting matrix \(\tilde A\) is much cheaper to invert.

The preconditioner is

\[P = R {\tilde A}^{-1} R^T\]

with an averagingn operator \(R\).

mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
for l in range(3): mesh.Refine()
fes = H1(mesh, order=10, dirichlet=".*")
print ("ndof =", fes.ndof)

u, v = fes.TnT()
with TaskManager():
    a = BilinearForm(grad(u)*grad(v)*dx+u*v*dx)
    pre = Preconditioner(a, "bddc")
    a.Assemble()
    f = LinearForm(x*v*dx).Assemble()

gfu = GridFunction(fes)
with TaskManager():
    inv = CGSolver(a.mat, pre, maxsteps=2000, printrates=False)
    ts = time()
    gfu.vec.data = (inv * f.vec).Evaluate()
    te = time()
    print ("iterations =", inv.GetSteps(), "time =", te-ts)

 Mesh bisection
 Bisection done
 Mesh bisection
 Bisection done
 Mesh bisection
 Bisection done
ndof = 737601
iterations = 52 time = 3.381578207015991

predev = pre.mat.CreateDeviceMatrix()
print (predev.GetOperatorInfo())

SumMatrix, h = 737601, w = 737601
  ProductMatrix, h = 737601, w = 737601
    ProductMatrix, h = 737601, w = 737601
      SparseMatrixd, h = 737601, w = 737601
      SparseCholesky-d, h = 737601, w = 737601
    SparseMatrixd, h = 737601, w = 737601
  SparseMatrixd, h = 737601, w = 737601

adev = a.mat.CreateDeviceMatrix()
predev = pre.mat.CreateDeviceMatrix()
fdev = f.vec.CreateDeviceVector()

with TaskManager():
    inv = CGSolver(adev, predev, maxsteps=2000, printrates=False)
    gfu.vec.data = (inv * fdev).Evaluate()
    print ("iterations =", inv.GetSteps())

No device creator function, creating host vector
iterations = 52

A100: iterations = 53 time= 0.16417622566223145

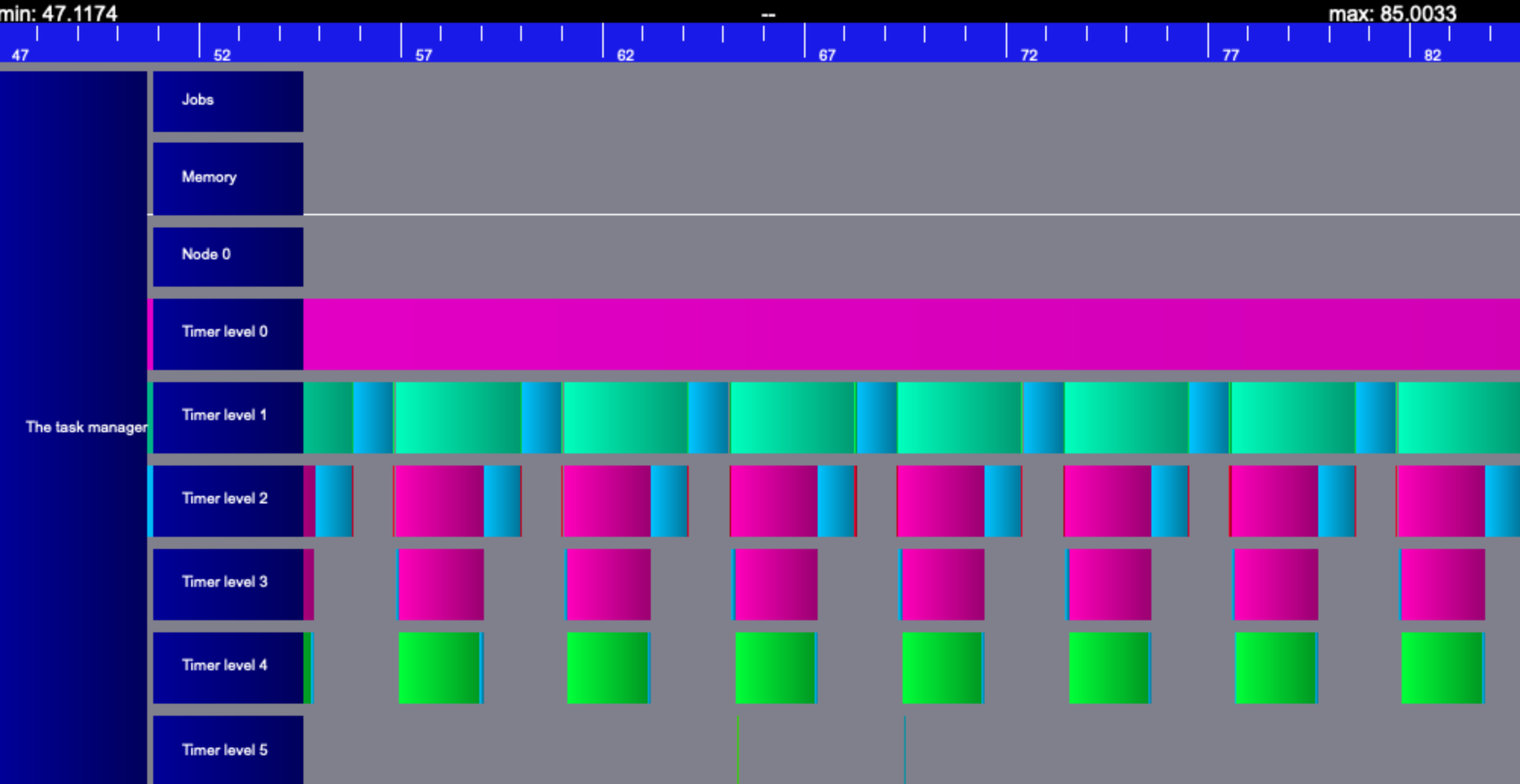
Vite - traces: