This page was generated from historic/unit-5.2-fetidp_point2d/feti-dp-i.ipynb.
5.6.1 FETI-DP in NGSolve I: Working with Point-Constraints¶
We implement standard FETI-DP, using only point-constraints, for Poisson’s equation, in 2D.
This is easily done with NGS-Py, because:
We need access to sub-assembled matrices for each subdomain, which is exactly how matrices are stored in NGSolve.
In fact, we can just reuse these local matrices for the dual-primal space.
We do not need to concern ourselves with finding any sort of global enumeration in the dual-primal space, because NGSolve does not work with one. We only need ParallelDofs for the dual-primal space.
Use the cells at the bottom of this file to experiment with bigger computations!¶
[1]:
num_procs = '40'
[2]:
from usrmeeting_jupyterstuff import *
[ ]:
stop_cluster()
[3]:
start_cluster(num_procs)
connect_cluster()
Waiting for connection file: ~/.ipython/profile_ngsolve/security/ipcontroller-kogler-client.json
connecting ... try:6 succeeded!
[4]:
%%px
from ngsolve import *
import netgen.meshing as ngmeshing
comm = MPI_Init()
nref = 1
ngmesh = ngmeshing.Mesh(dim=2)
ngmesh.Load('squaref.vol')
for l in range(nref):
ngmesh.Refine()
mesh = Mesh(ngmesh)
comm = MPI_Init()
fes = H1(mesh, order=2, dirichlet='right|top')
a = BilinearForm(fes)
u,v = fes.TnT()
a += SymbolicBFI(grad(u)*grad(v))
a.Assemble()
f = LinearForm(fes)
f += SymbolicLFI(x*y*v)
f.Assemble()
avg_dof = comm.Sum(fes.ndof) / comm.size
if comm.rank==0:
print('global, ndof =', fes.ndofglobal, ', lodofs =', fes.lospace.ndofglobal)
print('avg DOFs per core: ', avg_dof)
[stdout:10]
global, ndof = 187833 , lodofs = 47161
avg DOFs per core: 4823.075
Finding the primal DOFs¶
First, we have to find out which DOFs sit on subdomain vertices.
In 2 dimensions, those are just the ones that are shared between 3 or more ranks.
Additionally, we only need to concern ourselves with non-dirichlet DOFs.
We simply construct a BitArray, which is True wherever we have a primal DOF, and else False.
[5]:
%%px
primal_dofs = BitArray([len(fes.ParallelDofs().Dof2Proc(k))>1 for k in range(fes.ndof)]) & fes.FreeDofs()
nprim = comm.Sum(sum([1 for k in range(fes.ndof) if primal_dofs[k] \
and comm.rank<fes.ParallelDofs().Dof2Proc(k)[0] ]))
npmin = comm.Min(primal_dofs.NumSet() if comm.rank else nprim)
npavg = comm.Sum(primal_dofs.NumSet())/comm.size
npmax = comm.Max(primal_dofs.NumSet())
if comm.rank==0:
print('# primal dofs global: ', nprim)
print('min, avg, max per rank: ', npmin, npavg, npmax)
[stdout:10]
# primal dofs global: 56
min, avg, max per rank: 1 4.225 7
Setting up the Dual-Primal-Space Matrix¶
We want to assemble the stiffness-matrix on the dual-primal space
This means that we need:
local stiffness matrices:
ParallelDofs
If we restrict \(V_{\scriptscriptstyle DP}\) to some subdomain, we get the same space we get from restricting \(V\), so the local matrices are the same!
The coupling of DOFs between the subdomains is now different. We need to construct new ParallelDofs
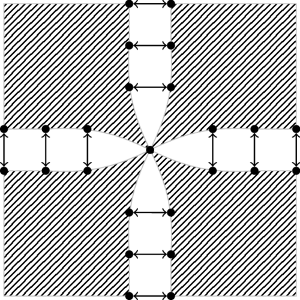
If we think of ParallelDofs as the connection between DOFs of different subdomains, the dual-primal ParallelDofs are simply a subset of the ones in the primal space.
[6]:
%%px
dp_pardofs = fes.ParallelDofs().SubSet(primal_dofs)
if comm.rank==0:
print('global ndof in original space : ', fes.ParallelDofs().ndofglobal)
print('global ndof in dual-primal space: ', dp_pardofs.ndofglobal)
[stdout:10]
global ndof in original space : 187833
global ndof in dual-primal space: 192810
The ParallelMatrix for the DP-Space¶
A ParallelMatrix is just a local matrix + ParallelDofs. We have access to both.
[7]:
%%px
from ngsolve.la import ParallelMatrix
A_dp = ParallelMatrix(a.mat.local_mat, dp_pardofs)
A_dp_inv = A_dp.Inverse(fes.FreeDofs(), inverse='mumps')
The Jump-Operator \(B\)¶
The Jump-operator is implemented on C++-side. The constraints are fully redundant. The jump operator builds constraints for all connections in the given ParallelDofs. In our case, we only need the constraints for the non-primal DOFs.
In order for CreateRowVector to be properly defined, the jump-operator has to be told in which space the "u-vectors" live.
This is done by setting "u_pardofs". If none are given, or they are explicitly given as "None", B assumes a fully discontinuous u-space.
[8]:
%%px
from ngsolve.la import FETI_Jump
dual_pardofs = fes.ParallelDofs().SubSet(BitArray(~primal_dofs & fes.FreeDofs()))
B = FETI_Jump(dual_pardofs, u_pardofs=dp_pardofs)
if comm.rank==0:
print('# of global multipliers = :', B.col_pardofs.ndofglobal)
elif comm.rank<10:
print('rank', comm.rank, ', # of local multipliers = ', B.col_pardofs.ndoflocal)
[stdout:1] rank 8 , # of local multipliers = 283
[stdout:2] rank 6 , # of local multipliers = 186
[stdout:4] rank 7 , # of local multipliers = 214
[stdout:7] rank 5 , # of local multipliers = 170
[stdout:9] rank 4 , # of local multipliers = 279
[stdout:10] # of global multipliers = : 4968
[stdout:12] rank 1 , # of local multipliers = 259
[stdout:14] rank 2 , # of local multipliers = 204
[stdout:15] rank 3 , # of local multipliers = 293
[stdout:17] rank 9 , # of local multipliers = 287
Forming the Schur-Complement¶
We can very easily define the (negative) Schur-Complement \(F = B~A_{\scriptscriptstyle DP}^{-1}~B^T\) with the "@"-operator.
"@" can concatenate any operators of "BaseMatrix" type. They have to provide a Mult method as well as CreateRow/ColVector, which is needed to construct vectors to store intermediate vectors.
[9]:
%%px
F = B @ A_dp_inv @ B.T
if comm.rank==0:
print('type F: ', type(F))
[stdout:10] type F: <class 'ngsolve.la.BaseMatrix'>
The Preconditioner¶
The Dirichlet-Preconditioner can also be written down very easily.
We have, with B standing for border DOFs, and I standing for inner DOFs,
The inner part, the Dirichlet-to-Neumann Schur-Complement, can be implemented with a small trick:
:nbsphinx-math:`begin{align*} left(begin{matrix} A_{BB} & A_{BI} \ A_{IB} & A_{II} end{matrix}right) cdot left[ left(begin{matrix} I & 0\ 0 & I end{matrix}right) - left(begin{matrix} 0 & 0\ 0 & A_{II}^{-1} end{matrix}right) cdot left(begin{matrix} A_{BB} & A_{BI} \ A_{IB} & A_{II} end{matrix}right) right] & = left(begin{matrix} A_{BB} & A_{BI} \ A_{IB} & A_{II} end{matrix}right) cdot left[ left(begin{matrix} I & 0\ 0 & I end{matrix}right) - left(begin{matrix} 0 & 0\ A_{II}^{-1}A_{IB} & I end{matrix}right) right]
= \ =
left(begin{matrix} A_{BB} & A_{BI} \ A_{IB} & A_{II} end{matrix}right) cdot left(begin{matrix} I & 0\ -A_{II}^{-1}A_{IB} & 0 end{matrix}right) & = left(begin{matrix} A_{BB} - A_{BI}A_{II}^{-1}A_{IB} & 0\ 0 & 0 end{matrix}right) end{align*}`
[10]:
%%px
innerdofs = BitArray([len(fes.ParallelDofs().Dof2Proc(k))==0 for k in range(fes.ndof)]) & fes.FreeDofs()
A = a.mat.local_mat
Aiinv = A.Inverse(innerdofs, inverse='sparsecholesky')
Fhat = B @ A @ (IdentityMatrix() - Aiinv @ A) @ B.T
Multiplicity Scaling¶
The scaled Dirichlet-Preconditioner is just
where
and \(D = \text{diag}([\text{multiplicity of DOF }i\text{ }: i=0\ldots n-1])\).
We can implement this without untroducing D as a matrix, and thus avoiding copying of entries.
[11]:
%%px
class ScaledMat(BaseMatrix):
def __init__ (self, A, vals):
super(ScaledMat, self).__init__()
self.A = A
self.scaledofs = [k for k in enumerate(vals) if k[1]!=1.0]
def CreateRowVector(self):
return self.A.CreateRowVector()
def CreateColVector(self):
return self.A.CreateColVector()
def Mult(self, x, y):
y.data = self.A * x
for k in self.scaledofs:
y[k[0]] *= k[1]
scaledA = ScaledMat(A, [1.0/(1+len(fes.ParallelDofs().Dof2Proc(k))) for k in range(fes.ndof)])
scaledBT = ScaledMat(B.T, [1.0/(1+len(fes.ParallelDofs().Dof2Proc(k))) for k in range(fes.ndof)])
Fhat2 = B @ scaledA @ (IdentityMatrix() - Aiinv @ A) @ scaledBT
Prepare RHS¶
[12]:
%%px
hv = B.CreateRowVector()
rhs = B.CreateColVector()
lam = B.CreateColVector()
hv.data = A_dp_inv * f.vec
rhs.data = B * hv
Solve for \(\lambda\) - without scaling¶
[13]:
%%px
tsolve1 = -comm.WTime()
solvers.CG(mat=F, pre=Fhat, rhs=rhs, sol=lam, maxsteps=100, printrates=comm.rank==0, tol=1e-6)
tsolve1 += comm.WTime()
if comm.rank==0:
print('time to solve =', tsolve1)
[stdout:10]
it = 0 err = 0.33241357601342986
it = 1 err = 0.08073724692259508
it = 2 err = 0.03342603729269669
it = 3 err = 0.018590695356589717
it = 4 err = 0.0059947474548240785
it = 5 err = 0.0027638282106529502
it = 6 err = 0.0014339187849704818
it = 7 err = 0.0005940409981120754
it = 8 err = 0.0003125855268094198
it = 9 err = 0.0001315943979595822
it = 10 err = 5.087321086144511e-05
it = 11 err = 2.259284681093829e-05
it = 12 err = 8.338649672536656e-06
it = 13 err = 3.884661119865966e-06
it = 14 err = 1.5186884566911164e-06
it = 15 err = 6.629027204434754e-07
time to solve = 0.5055452309316024
Solve for \(\lambda\) - with scaling¶
[14]:
%%px
tsolve2 = -comm.WTime()
solvers.MinRes(mat=F, pre=Fhat2, rhs=rhs, sol=lam, maxsteps=100, printrates=comm.rank==0, tol=1e-6)
tsolve2 += comm.WTime()
if comm.rank==0:
print('time to solve =', tsolve2)
[stdout:10]
it = 0 err = 0.16620678800671493
it = 1 err = 0.03922813647750846
it = 2 err = 0.015375708271880666
it = 3 err = 0.007954691011138264
it = 4 err = 0.0028048597514098014
it = 5 err = 0.001239627101399431
it = 6 err = 0.0006206316326847184
it = 7 err = 0.00026791930129006525
it = 8 err = 0.00013500096491957006
it = 9 err = 5.9146271053553835e-05
it = 10 err = 2.3367293859660653e-05
it = 11 err = 1.0170342441937255e-05
it = 12 err = 3.857744385789025e-06
it = 13 err = 1.7348456034200445e-06
it = 14 err = 6.956273460897132e-07
time to solve = 0.4004018809646368
A faster dual-primal Inverse¶
We just inverted \(A_{\scriptscriptstyle DP}\) with MUMPS, and while this is faster than inverting \(A\), in practice this is not scalable.
MUMPS does not realize that it can eliminate all of the dual DOFs locally.
We can implement a much faster, and more scalable, dual-primal inverse per hand. For that, we reduce the problem to the Schur-complement with resprect to the primal DOFs using local sparse matrix factorization, and then only invert the primal schur-complement \(S_{\pi\pi}\) globally.
In order to globally invert \(S_{\pi\pi}\), we need its local sub-matrix as a sparse matrix, not as the expression
A @ (IdentityMatrix() - All_inv @ A)
For that, we can just repeatedly multiply unit vectors.
[15]:
%%px
from dd_toolbox import Op2SPM
class LocGlobInverse(BaseMatrix):
def __init__ (self, Aglob, freedofs, invtype_loc='sparsecholesky',\
invtype_glob='masterinverse'):
super(LocGlobInverse, self).__init__()
self.Aglob = Aglob
self.A = Aglob.local_mat
pardofs = Aglob.col_pardofs
local_dofs = BitArray([len(pardofs.Dof2Proc(k))==0 for k in range(pardofs.ndoflocal)]) & freedofs
global_dofs = BitArray(~local_dofs & freedofs)
self.All_inv = self.A.Inverse(local_dofs, inverse=invtype_loc)
sp_loc_asmult = self.A @ (IdentityMatrix() - self.All_inv @ self.A)
sp_loc = Op2SPM(sp_loc_asmult, global_dofs, global_dofs)
sp = ParallelMatrix(sp_loc, pardofs)
self.Sp_inv = sp.Inverse(global_dofs, inverse=invtype_glob)
self.tv = self.Aglob.CreateRowVector()
self.btilde = self.Aglob.CreateRowVector()
def CreateRowVector(self):
return self.Aglob.CreateRowVector()
def CreateColVector(self):
return self.CreateRowVector()
def Mult(self, b, u):
self.tv.data = self.All_inv * b
b.Distribute()
self.btilde.data = b - self.A * self.tv
u.data = self.Sp_inv * self.btilde
self.tv.data = b - self.A * u
u.data += self.All_inv * self.tv
[16]:
%%px
A_dp_inv2 = LocGlobInverse(A_dp, fes.FreeDofs(), \
'sparsecholesky', 'mumps')
F2 = B @ A_dp_inv2 @ B.T
Solve for \(\lambda\)¶
[17]:
%%px
tsolve1 = -comm.WTime()
solvers.CG(mat=F, pre=Fhat, rhs=rhs, sol=lam, maxsteps=100, printrates=comm.rank==0, tol=1e-6)
tsolve1 += comm.WTime()
if comm.rank==0:
print('')
tsolve2 = -comm.WTime()
solvers.CG(mat=F, pre=Fhat2, rhs=rhs, sol=lam, maxsteps=100, printrates=comm.rank==0, tol=1e-6)
tsolve2 += comm.WTime()
if comm.rank==0:
print('')
tsolve3 = -comm.WTime()
solvers.CG(mat=F2, pre=Fhat2, rhs=rhs, sol=lam, maxsteps=100, printrates=comm.rank==0, tol=1e-6)
tsolve3 += comm.WTime()
if comm.rank==0:
print('\ntime solve v1: ', tsolve1)
print('time solve v2: ', tsolve2)
print('time solve v3: ', tsolve3)
[stdout:10]
it = 0 err = 0.33241357601342986
it = 1 err = 0.08073724692259508
it = 2 err = 0.0334260372926967
it = 3 err = 0.018590695356589713
it = 4 err = 0.0059947474548240785
it = 5 err = 0.0027638282106529494
it = 6 err = 0.0014339187849704807
it = 7 err = 0.0005940409981120754
it = 8 err = 0.00031258552680941964
it = 9 err = 0.0001315943979595821
it = 10 err = 5.087321086144511e-05
it = 11 err = 2.2592846810938306e-05
it = 12 err = 8.33864967253665e-06
it = 13 err = 3.884661119865963e-06
it = 14 err = 1.5186884566911173e-06
it = 15 err = 6.629027204434756e-07
it = 0 err = 0.16620678800671493
it = 1 err = 0.04036862346129754
it = 2 err = 0.01671301864634835
it = 3 err = 0.009295347678294857
it = 4 err = 0.002997373727412039
it = 5 err = 0.0013819141053264743
it = 6 err = 0.0007169593924852402
it = 7 err = 0.0002970204990560376
it = 8 err = 0.00015629276340470955
it = 9 err = 6.5797198979791e-05
it = 10 err = 2.5436605430722535e-05
it = 11 err = 1.1296423405469144e-05
it = 12 err = 4.169324836268321e-06
it = 13 err = 1.94233055993298e-06
it = 14 err = 7.59344228345558e-07
it = 15 err = 3.3145136022173774e-07
it = 0 err = 0.16620678800671493
it = 1 err = 0.040368623461284836
it = 2 err = 0.016713018646346594
it = 3 err = 0.009295347678294864
it = 4 err = 0.002997373727412205
it = 5 err = 0.0013819141053272297
it = 6 err = 0.0007169593924864385
it = 7 err = 0.0002970204990560735
it = 8 err = 0.00015629276340464927
it = 9 err = 6.579719897977235e-05
it = 10 err = 2.54366054307179e-05
it = 11 err = 1.1296423405458421e-05
it = 12 err = 4.169324836254944e-06
it = 13 err = 1.942330559925504e-06
it = 14 err = 7.593442283447208e-07
it = 15 err = 3.3145136022149025e-07
time solve v1: 0.5127908659633249
time solve v2: 0.47894827101845294
time solve v3: 0.14496840198989958
Not that the normal and scaled variants of the Dirichlet-Preconditioner are equivalent here, because all DOFs are either local, primal, or shared by exactly two ranks.
Reconstruct \(u\)¶
[18]:
%%px
gfu = GridFunction(fes)
hv.data = f.vec - B.T * lam
gfu.vec.data = A_dp_inv * hv
jump = lam.CreateVector()
jump.data = B * gfu.vec
norm_jump = Norm(jump)
if comm.rank==0:
print('norm jump u: ', norm_jump)
[stdout:10] norm jump u: 2.7631462978367745e-07
[19]:
%%px --target 1
for t in sorted(filter(lambda t:t['time']>0.5, Timers()), key=lambda t:t['time'], reverse=True):
print(t['name'], ': ', t['time'])
Mumps Inverse : 2.067965030670166
Mumps Inverse - analysis : 1.8604109287261963
Parallelmumps mult inverse : 1.8263428211212158
[20]:
%%px
t_chol = filter(lambda t: t['name'] == 'SparseCholesky<d,d,d>::MultAdd', Timers()).__next__()
maxt = comm.Max(t_chol['time'])
if t_chol['time'] == maxt:
for t in sorted(filter(lambda t:t['time']>0.3*maxt, Timers()), key=lambda t:t['time'], reverse=True):
print(t['name'], ': ', t['time'])
[stdout:36]
Mumps Inverse : 2.035609245300293
Mumps Inverse - analysis : 1.8604459762573242
Parallelmumps mult inverse : 1.8067901134490967
SparseCholesky<d,d,d>::MultAdd : 0.1947925090789795
Mumps Inverse - factor : 0.1496748924255371
SparseCholesky<d,d,d>::MultAdd fac1 : 0.12263321876525879
SparseCholesky<d,d,d>::MultAdd fac2 : 0.06641483306884766
[21]:
stop_cluster()
Experiment Below!¶
[22]:
from usrmeeting_jupyterstuff import *
num_procs = '80'
start_cluster(num_procs)
connect_cluster()
Waiting for connection file: ~/.ipython/profile_ngsolve/security/ipcontroller-kogler-client.json
connecting ... try:6 succeeded!
[23]:
%%px
from ngsolve import *
import netgen.meshing as ngmeshing
from ngsolve.la import ParallelMatrix, FETI_Jump
from dd_toolbox import LocGlobInverse, ScaledMat
def load_mesh(nref=0):
ngmesh = ngmeshing.Mesh(dim=2)
ngmesh.Load('squaref.vol')
for l in range(nref):
ngmesh.Refine()
return Mesh(ngmesh)
def setup_space(mesh, order=1):
comm = MPI_Init()
fes = H1(mesh, order=order, dirichlet='right|top')
a = BilinearForm(fes)
u,v = fes.TnT()
a += SymbolicBFI(grad(u)*grad(v))
a.Assemble()
f = LinearForm(fes)
f += SymbolicLFI(x*y*v)
f.Assemble()
avg_dof = comm.Sum(fes.ndof) / comm.size
if comm.rank==0:
print('global, ndof =', fes.ndofglobal, ', lodofs =', fes.lospace.ndofglobal)
print('avg DOFs per core: ', avg_dof)
return [fes, a, f]
def setup_FETIDP(fes, a):
primal_dofs = BitArray([len(fes.ParallelDofs().Dof2Proc(k))>1 for k in range(fes.ndof)]) & fes.FreeDofs()
nprim = comm.Sum(sum([1 for k in range(fes.ndof) if primal_dofs[k] \
and comm.rank<fes.ParallelDofs().Dof2Proc(k)[0] ]))
if comm.rank==0:
print('# primal dofs global: ', nprim)
dp_pardofs = fes.ParallelDofs().SubSet(primal_dofs)
A_dp = ParallelMatrix(a.mat.local_mat, dp_pardofs)
A_dp_inv = A_dp.Inverse(fes.FreeDofs(), inverse='mumps')
dual_pardofs = fes.ParallelDofs().SubSet(BitArray(~primal_dofs & fes.FreeDofs()))
B = FETI_Jump(dual_pardofs, u_pardofs=dp_pardofs)
if comm.rank==0:
print('# of global multipliers = :', B.col_pardofs.ndofglobal)
F = B @ A_dp_inv @ B.T
A_dp_inv2 = LocGlobInverse(A_dp, fes.FreeDofs(), \
invtype_loc='sparsecholesky',\
invtype_glob='masterinverse')
F2 = B @ A_dp_inv2 @ B.T
innerdofs = BitArray([len(fes.ParallelDofs().Dof2Proc(k))==0 for k in range(fes.ndof)]) & fes.FreeDofs()
A = a.mat.local_mat
Aiinv = A.Inverse(innerdofs, inverse='sparsecholesky')
Fhat = B @ A @ (IdentityMatrix() - Aiinv @ A) @ B.T
scaledA = ScaledMat(A, [1.0/(1+len(fes.ParallelDofs().Dof2Proc(k))) for k in range(fes.ndof)])
scaledBT = ScaledMat(B.T, [1.0/(1+len(fes.ParallelDofs().Dof2Proc(k))) for k in range(fes.ndof)])
Fhat2 = B @ scaledA @ (IdentityMatrix() - Aiinv @ A) @ scaledBT
return [A_dp, A_dp_inv, A_dp_inv2, F, F2, Fhat, Fhat2, B, scaledA, scaledBT]
def prep(B, Ainv, f):
rhs.data = (B @ Ainv) * f.vec
return rhs
def solve(mat, pre, rhs, sol):
t = comm.WTime()
solvers.CG(mat=mat, pre=pre, rhs=rhs, sol=sol, \
maxsteps=100, printrates=comm.rank==0, tol=1e-6)
return comm.WTime() - t
def post(B, Ainv, gfu, lam):
hv = B.CreateRowVector()
hv.data = f.vec - B.T * lam
gfu.vec.data = Ainv * hv
jump = lam.CreateVector()
jump.data = B * gfu.vec
norm_jump = Norm(jump)
if comm.rank==0:
print('norm jump u: ', norm_jump)
[24]:
%%px
comm = MPI_Init()
mesh = load_mesh(nref=1)
fes, a, f = setup_space(mesh, order=2)
A_dp, A_dp_inv, A_dp_inv2, F, F2, Fhat, Fhat2, B, scaledA, scaledBT = setup_FETIDP(fes, a)
rhs = B.CreateColVector()
lam = B.CreateColVector()
prep(B, A_dp_inv2, f)
if comm.rank==0:
print('')
t1 = solve(F, Fhat, rhs, lam)
if comm.rank==0:
print('')
t2 = solve(F, Fhat2, rhs, lam)
if comm.rank==0:
print('')
t3 = solve(F2, Fhat2, rhs, lam)
if comm.rank==0:
print('\ntime solve v1: ', t1)
print('time solve v2: ', t2)
print('time solve v3: ', t3)
gfu = GridFunction(fes)
post(B, A_dp_inv2, gfu, lam)
[stdout:1]
global, ndof = 187833 , lodofs = 47161
avg DOFs per core: 2441.0875
# primal dofs global: 125
# of global multipliers = : 7188
it = 0 err = 0.2775003436443844
it = 1 err = 0.059395434678847045
it = 2 err = 0.02668466647171506
it = 3 err = 0.013658995259387977
it = 4 err = 0.0049131733239784845
it = 5 err = 0.0021229848364316215
it = 6 err = 0.0009537456623955999
it = 7 err = 0.0003609947384913908
it = 8 err = 0.0001589874932742381
it = 9 err = 6.398790188681329e-05
it = 10 err = 2.5454548026516644e-05
it = 11 err = 9.979151075046508e-06
it = 12 err = 4.614085390943377e-06
it = 13 err = 1.8339700212425154e-06
it = 14 err = 7.44343568078797e-07
it = 15 err = 3.473053788503813e-07
it = 0 err = 0.1387501718221922
it = 1 err = 0.029697717339423522
it = 2 err = 0.01334233323585753
it = 3 err = 0.006829497629693989
it = 4 err = 0.002456586661989242
it = 5 err = 0.0010614924182158108
it = 6 err = 0.00047687283119779986
it = 7 err = 0.00018049736924569538
it = 8 err = 7.949374663711905e-05
it = 9 err = 3.1993950943406623e-05
it = 10 err = 1.2727274013258324e-05
it = 11 err = 4.989575537523253e-06
it = 12 err = 2.3070426954716886e-06
it = 13 err = 9.169850106212577e-07
it = 14 err = 3.721717840393986e-07
it = 15 err = 1.7365268942519067e-07
it = 0 err = 0.1387501718221922
it = 1 err = 0.02969771733942429
it = 2 err = 0.013342333235858251
it = 3 err = 0.006829497629693326
it = 4 err = 0.002456586661989025
it = 5 err = 0.0010614924182156267
it = 6 err = 0.00047687283119771643
it = 7 err = 0.00018049736924568807
it = 8 err = 7.949374663711586e-05
it = 9 err = 3.19939509434018e-05
it = 10 err = 1.2727274013256248e-05
it = 11 err = 4.98957553752233e-06
it = 12 err = 2.3070426954715653e-06
it = 13 err = 9.16985010621377e-07
it = 14 err = 3.7217178403948777e-07
it = 15 err = 1.736526894252284e-07
time solve v1: 0.4511956589994952
time solve v2: 0.48503338207956403
time solve v3: 0.06109175400342792
norm jump u: 1.0723427980831504e-07
[25]:
%%px --target 1
for t in sorted(filter(lambda t:t['time']>0.5, Timers()), key=lambda t:t['time'], reverse=True):
print(t['name'], ': ', t['time'])
Mumps Inverse : 2.0638580322265625
Mumps Inverse - analysis : 1.8557240962982178
Parallelmumps mult inverse : 0.8613486289978027
[26]:
%%px
t_chol = filter(lambda t: t['name'] == 'SparseCholesky<d,d,d>::MultAdd', Timers()).__next__()
maxt = comm.Max(t_chol['time'])
if t_chol['time'] == maxt:
print('timers from rank ', comm.rank, ':')
for t in sorted(filter(lambda t:t['time']>min(0.3*maxt, 0.5), Timers()), key=lambda t:t['time'], reverse=True):
print(t['name'], ': ', t['time'])
[stdout:12]
timers from rank 14 :
Mumps Inverse : 2.063915967941284
Mumps Inverse - analysis : 1.855010986328125
Parallelmumps mult inverse : 0.8388888835906982
dummy - AllReduce : 0.26943492889404297
Mumps Inverse - factor : 0.19652891159057617
dummy - AllReduce : 0.08971333503723145
SparseCholesky<d,d,d>::MultAdd : 0.059799909591674805
SparseCholesky<d,d,d>::MultAdd fac1 : 0.03657698631286621
SparseCholesky<d,d,d>::MultAdd fac2 : 0.021203994750976562
SparseCholesky - total : 0.019064903259277344
[27]:
stop_cluster()