This page was generated from wta/elasticity3D.ipynb.

3D Solid Mechanics

• Open Cascade Techonology geometry kernel

• Netgen mesh generator

• NGSolve Finite Element libraray

from netgen.occ import *
from ngsolve import *
from ngsolve.webgui import Draw

box = Box((0,0,0), (3,0.6,1))
box.faces.name="outer"
cyl = sum( [Cylinder((0.5+i,0,0.5), Y, 0.25,0.8) for i in range(3)] )
cyl.faces.name="cyl"
geo = box-cyl

ea = { "euler_angles" : [-70,5,30] }
Draw(geo, **ea);

find edges between box and cylinder, and build chamfers:

cylboxedges = geo.faces["outer"].edges * geo.faces["cyl"].edges
cylboxedges.name = "cylbox"
geo = geo.MakeChamfer(cylboxedges, 0.03)

name faces for boundary conditions:

geo.faces.Min(X).name = "fix"
geo.faces.Max(X).name = "force"

Draw(geo, **ea);

mesh = geo.GenerateMesh(maxh=0.1).Curve(3)
Draw (mesh, **ea);

Linear elasticity

Displacement: $u:\mathrm{\Omega }\to {\mathbb{R}}^3$

Linear strain:

$$\epsilon (u):=\frac{1}{2}(\mathrm{\nabla }u+(\mathrm{\nabla }u{)}^T)$$

Stress by Hooke’s law:

$$\sigma =2\mu \epsilon +\lambda \mathrm{tr}\epsilon I$$

Equilibrium of forces:

$$\mathrm{div}\sigma =f$$

Displacement boundary conditions:

$$u=u_D\text{on}{\mathrm{\Gamma }}_D$$

Traction boundary conditions:

$$\sigma n=g\text{on}{\mathrm{\Gamma }}_N$$

Variational formulation:

Find: $u\in H^1(\mathrm{\Omega }{)}^3$ such that $u=u_D$ on ${\mathrm{\Gamma }}_D$

$${\int }_{\mathrm{\Omega }}\sigma (\epsilon (u)):\epsilon (v)dx={\int }_{\mathrm{\Omega }}fvdx+{\int }_{{\mathrm{\Gamma }}_N}gvds$$

holds for all $v=0$ on ${\mathrm{\Gamma }}_D$.

E, nu = 210, 0.2
mu  = E / 2 / (1+nu)
lam = E * nu / ((1+nu)*(1-2*nu))

def Stress(strain):
    return 2*mu*strain + lam*Trace(strain)*Id(3)

fes = VectorH1(mesh, order=3, dirichlet="fix")
u,v = fes.TnT()
gfu = GridFunction(fes)

with TaskManager():
    a = BilinearForm(InnerProduct(Stress(Sym(Grad(u))), Sym(Grad(v))).Compile()*dx)
    pre = preconditioners.BDDC(a)
    a.Assemble()

force = CF( (1e-3,0,0) )
f = LinearForm(force*v*ds("force")).Assemble()

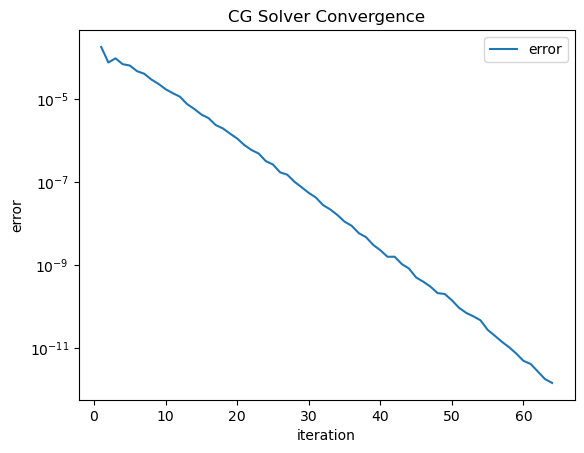
inv = solvers.CGSolver(a.mat, pre, plotrates=True, tol=1e-8)
gfu.vec.data = inv * f.vec

<Figure size 640x480 with 0 Axes>

with TaskManager():
    fesstress = MatrixValued(H1(mesh,order=3), symmetric=True)
    gfstress = GridFunction(fesstress)
    gfstress.Interpolate (Stress(Sym(Grad(gfu))))

Draw (gfu, mesh, deformation=True, scale=3e4, draw_vol=False, **ea);

Draw (Norm(gfstress), mesh, deformation=1e4*gfu, draw_vol=False, order=3, **ea);