This page was generated from wta/coil.ipynb.

Magnetostatics

from netgen.occ import *
from ngsolve import *
from ngsolve.webgui import Draw
from netgen.webgui import Draw as DrawGeo
import math

model of the coil:

cyl = Cylinder((0,0,0), Z, r=0.01, h=0.03).faces[0]
heli = Edge(Segment((0,0), (12*math.pi, 0.03)), cyl)
ps = heli.start
vs = heli.start_tangent
pe = heli.end
ve = heli.end_tangent

e1 = Segment((0,0,-0.03), (0,0,-0.01))
c1 = BezierCurve( [(0,0,-0.01), (0,0,0), ps-vs, ps])
e2 = Segment((0,0,0.04), (0,0,0.06))
c2 = BezierCurve( [pe, pe+ve, (0,0,0.03), (0,0,0.04)])
spiral = Wire([e1, c1, heli, c2, e2])
circ = Face(Wire([Circle((0,0,-0.03), Z, 0.001)]))
coil = Pipe(spiral, circ)

coil.faces.maxh=0.2
coil.faces.name="coilbnd"
coil.faces.Max(Z).name="in"
coil.faces.Min(Z).name="out"
coil.mat("coil")
crosssection = coil.faces.Max(Z).mass

DrawGeo (coil);

box = Box((-0.04,-0.04,-0.03), (0.04,0.04,0.06))
box.faces.name = "outer"
air = box-coil
air.mat("air");

mesh-generation of coil and air-box:

geo = OCCGeometry(Glue([coil,air]))
with TaskManager():
    mesh = Mesh(geo.GenerateMesh(meshsize.coarse, maxh=0.01)).Curve(3)

Draw (mesh, clipping={"y":1, "z":0, "dist":0.012});

checking mesh data materials and boundaries:

mesh.ne, mesh.nv, mesh.GetMaterials(), mesh.GetBoundaries()

(102331,
 17602,
 ('coil', 'air'),
 ('out',
  'coilbnd',
  'coilbnd',
  'coilbnd',
  'coilbnd',
  'coilbnd',
  'in',
  'outer',
  'outer',
  'outer',
  'outer',
  'outer',
  'outer'))

Solve a potential problem to determine current density in wire:

on the domain \(\Omega_{\text{coil}}\): \begin{eqnarray*} j & = & \sigma \nabla \Phi \\ \operatorname{div} j & = & 0 \end{eqnarray*} port boundary conditions: \begin{eqnarray*} \Phi & = & 0 \qquad \qquad \text{on } \Gamma_{\text{out}}, \\ j_n & = & \frac{1}{|S|} \quad \qquad \text{on } \Gamma_{\text{in}}, \end{eqnarray*} and \(j_n=0\) else

fespot = H1(mesh, order=3, definedon="coil", dirichlet="out")
phi,psi = fespot.TnT()
sigma = 58.7e6
bfa = BilinearForm(sigma*grad(phi)*grad(psi)*dx).Assemble()
inv = bfa.mat.Inverse(freedofs=fespot.FreeDofs(), inverse="sparsecholesky")
lff = LinearForm(1/crosssection*psi*ds("in")).Assemble()
gfphi = GridFunction(fespot)
gfphi.vec.data = inv * lff.vec

Draw (gfphi, draw_vol=False, clipping={"y":1, "z":0, "dist":0.012});

Solve magnetostatic problem:

current source is current from potential equation:

\[\int \mu^{-1} \operatorname{curl} u \cdot \operatorname{curl} v \, dx = \int j \cdot v \, dx\]

fes = HCurl(mesh, order=2, nograds=True)
print ("HCurl dofs:", fes.ndof)
u,v = fes.TnT()
mu = 4*math.pi*1e-7
a = BilinearForm(1/mu*curl(u)*curl(v)*dx+1e-6/mu*u*v*dx)
pre = Preconditioner(a, "bddc")
f = LinearForm(sigma*grad(gfphi)*v*dx("coil"))
with TaskManager():
    a.Assemble()
    f.Assemble()

HCurl dofs: 530978

from ngsolve.krylovspace import CGSolver
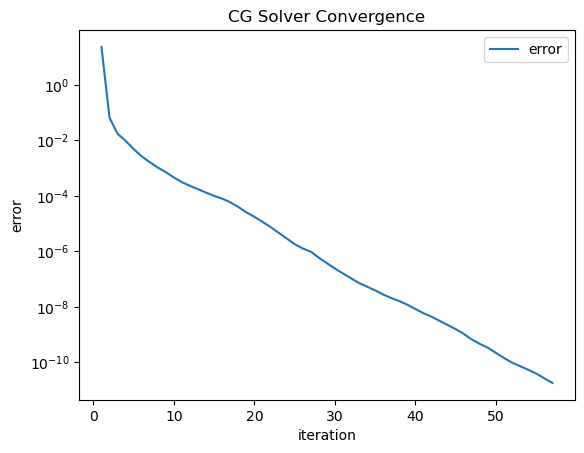
inv = CGSolver(a.mat, pre, printrates=True)
gfu = GridFunction(fes)
with TaskManager():
    gfu.vec.data = inv * f.vec

CG iteration 1, residual = 22.87001659123182
CG iteration 2, residual = 0.06721433407683128
CG iteration 3, residual = 0.01690890027778124
CG iteration 4, residual = 0.009408005471033747
CG iteration 5, residual = 0.004746471180398684
CG iteration 6, residual = 0.0026008223353248547
CG iteration 7, residual = 0.0016126286484539798
CG iteration 8, residual = 0.0010326981251104596
CG iteration 9, residual = 0.0007196103954447949
CG iteration 10, residual = 0.00046614993241146115
CG iteration 11, residual = 0.00032610321279847817
CG iteration 12, residual = 0.0002458584459419052
CG iteration 13, residual = 0.00019088906868810901
CG iteration 14, residual = 0.00014496102053837
CG iteration 15, residual = 0.00010840530408155666
CG iteration 16, residual = 8.372983852016451e-05
CG iteration 17, residual = 6.070427668740203e-05
CG iteration 18, residual = 4.022320497725715e-05
CG iteration 19, residual = 2.5303947740585147e-05
CG iteration 20, residual = 1.7280540420648763e-05
CG iteration 21, residual = 1.1395130811169012e-05
CG iteration 22, residual = 7.3792280042370286e-06
CG iteration 23, residual = 4.584471200088203e-06
CG iteration 24, residual = 2.8556674636352525e-06
CG iteration 25, residual = 1.7912501735229491e-06
CG iteration 26, residual = 1.3133353247972054e-06
CG iteration 27, residual = 9.503513366396761e-07
CG iteration 28, residual = 5.727818217012682e-07
CG iteration 29, residual = 3.673778734975989e-07
CG iteration 30, residual = 2.3676153553319604e-07
CG iteration 31, residual = 1.5897464753391983e-07
CG iteration 32, residual = 1.0700992799460232e-07
CG iteration 33, residual = 7.310590491053977e-08
CG iteration 34, residual = 5.494068543898494e-08
CG iteration 35, residual = 4.0714768965048847e-08
CG iteration 36, residual = 2.9081818332946315e-08
CG iteration 37, residual = 2.2055463894096586e-08
CG iteration 38, residual = 1.67369191585887e-08
CG iteration 39, residual = 1.2063882048224254e-08
CG iteration 40, residual = 8.541162800637749e-09
CG iteration 41, residual = 6.1792069121352095e-09
CG iteration 42, residual = 4.3623706823482986e-09
CG iteration 43, residual = 3.0331859881564403e-09
CG iteration 44, residual = 2.283662110711907e-09
CG iteration 45, residual = 1.5589836697879805e-09
CG iteration 46, residual = 1.0219779793091922e-09
CG iteration 47, residual = 6.610760048890652e-10
CG iteration 48, residual = 4.841337797842539e-10
CG iteration 49, residual = 3.3313349328210264e-10
CG iteration 50, residual = 2.123206156656037e-10
CG iteration 51, residual = 1.3926380471257822e-10
CG iteration 52, residual = 9.609859480748653e-11
CG iteration 53, residual = 7.282025035893849e-11
CG iteration 54, residual = 5.3481487529722107e-11
CG iteration 55, residual = 3.824877101414995e-11
CG iteration 56, residual = 2.5781211109897353e-11
CG iteration 57, residual = 1.757765470312381e-11

Draw (curl(gfu), mesh, draw_surf=False, \
      min=0, max=3e-4, clipping = { "y":1, "z" : 0, "function":False}, vectors = { "grid_size":100});