This page was generated from unit-3.8-simplehyp/shallow2D.ipynb.
3.8 A Nonlinear conservation law: shallow water equation in 2D¶
We consider the shallow water equations as an example of a nonlinear conservation law, i.e. we consider
with
and
Jacobian of the flux for shallow water:¶
\begin{align*} \mathbf{A}_1 & = \left(\begin{array}{ccc} 0 & 1 & 0 \\ - \frac{\mathbf{u}_2^2}{\mathbf{u}_1^2} + g \mathbf{u}_1 & 2 \frac{\mathbf{u}_2}{\mathbf{u}_1} & 0 \\ - \frac{\mathbf{u}_2 \mathbf{u}_3}{\mathbf{u}_1^2} & \frac{\mathbf{u}_3}{\mathbf{u}_1} & \frac{\mathbf{u}_2}{\mathbf{u}_1} \end{array} \right) = \left( \begin{array}{ccc} 0 & 1 & 0 \\ - u^2 + g h & 2 u & 0 \\ - u v & v & u \end{array} \right) \end{align*}
\begin{align*} \mathbf{A}_2 & = \left( \begin{array}{ccc} 0 & 0 & 1 \\ - \frac{\mathbf{u}_2\mathbf{u}_3}{\mathbf{u}_1^2} & \frac{\mathbf{u}_3}{\mathbf{u}_1} & \frac{\mathbf{u}_2}{\mathbf{u}_1} \\ - \frac{\mathbf{u}_3^2}{\mathbf{u}_1^2} + g \mathbf{u}_1 & 0 & 2\frac{\mathbf{u}_3}{\mathbf{u}_1} \end{array} \right) = \left( \begin{array}{ccc} 0 & 0 & 1 \\ - uv & v & u \\ - v^2 + gh & 0 & 2 v \end{array} \right) \end{align*}
\begin{align*} \mathbf{A}(\mathbf{u}, \mathbf{n}) & = n_1 \mathbf{A}_1 + n_2 \mathbf{A}_2 = \left( \begin{array}{ccc} 0 & n_1 & n_2 \\ - u \alpha - g h n_1 & \alpha + u n_1 & u n_2 \\ - v \alpha - g h n_2 & v n_1 & \alpha + v n_2 \end{array} \right), \quad \text{ with } \alpha = (\mathbf{u}, \mathbf{n}), \end{align*}
The dam break problem (geometry)¶
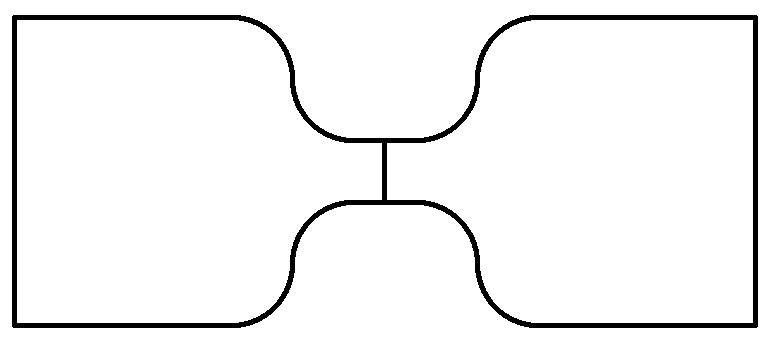
[1]:
# geometry description (including boundary/mat names)
from ngsolve import *
from netgen.occ import *
from ngsolve.webgui import *
wp = WorkPlane()
wp.MoveTo(-12,-5).LineTo(-3,-5).NameVertex("fillet")
wp.LineTo(-3,-1).NameVertex("fillet")
wp.LineTo(0,-1).LineTo(0,0).LineTo(-12,0).Close()
geo = wp.Face()
geo = geo.MakeFillet(list(set(geo.vertices["fillet"])),2)
geo = geo + geo.Mirror(Axis((0,0,0),X)).Reversed()
geo = Glue([geo,geo.Mirror(Axis((0,0,0),Y)).Reversed()])
geo.faces.Min(X).name="upperlevel"
geo.faces.Max(X).name="lowerlevel"
geo.edges.name = "wall"
geo.edges.Nearest((0,0)).name = "dam"
#Draw(geo)
geo = OCCGeometry(geo,dim=2)
[2]:
from ngsolve import *
from ngsolve.webgui import Draw
mesh = Mesh(geo.GenerateMesh(maxh=2))
mesh.Curve(3)
Draw(mesh)
[2]:
BaseWebGuiScene
Vectorial (dim=3) approximation space:¶
[3]:
order = 2
fes = L2(mesh,order=order)**3
#fes = L2(mesh,order=order,dim=3)
initial and boundary conditions¶
[4]:
U,V = fes.TnT() # "Trial" and "Test" function
h, hu, hv = U
# initial conditions
h0mat = {"upperlevel" : 10, "lowerlevel" : 2}
U0 = CF((mesh.MaterialCF(h0mat),0,0))
# boundary conditions
hbndreg = mesh.BoundaryCF({"wall" : h, "dam" : 0})
hubndreg = mesh.BoundaryCF({"wall" : -hu, "dam" : 0})
hvbndreg = mesh.BoundaryCF({"wall" : -hv, "dam" : 0})
Ubnd = CF((hbndreg,hubndreg,hvbndreg))
# constant for gravitational force
g=1
Flux definition and numerical flux choice (Lax-Friedrich)¶
[5]:
def F(U):
h, hvx, hvy = U
vx = hvx/h
vy = hvy/h
return CF(((hvx,hvy),
(hvx*vx + 0.5*g*h**2, hvx*vy),
(hvx*vy, hvy*vy + 0.5*g*h**2)),dims=(3,2))
[6]:
n = specialcf.normal(mesh.dim)
def Max(u,v):
return IfPos(u-v,u,v)
def Fmax(A,B): # max. characteristic speed:
ha, hua, hva = A
hb, hub, hvb = B
vnorma = sqrt(hua**2+hva**2)/ha
vnormb = sqrt(hub**2+hvb**2)/hb
return Max(vnorma+sqrt(g*A[0]),vnormb+sqrt(g*B[0]))
def Fhatn(U): # numerical flux
Uhat = U.Other(bnd=Ubnd)
return (0.5*F(U)+0.5*F(Uhat))*n + Fmax(U,Uhat)/2*(U-Uhat)
DG formulation¶
We recall that a BilinearForm is allowed to be nonlinear in the first argument.
[7]:
def DGBilinearForm(fes,F,Fhatn,Ubnd):
a = BilinearForm(fes, nonassemble=True)
a += - InnerProduct(F(U),Grad(V)) * dx
a += InnerProduct(Fhatn(U),V) * dx(element_boundary=True)
return a
a = DGBilinearForm(fes,F,Fhatn,Ubnd)
Simple fix to deal with shocks: artificial diffusion:¶
[8]:
from DGdiffusion import AddArtificialDiffusion
artvisc = Parameter(1.0)
if order > 0:
AddArtificialDiffusion(a,Ubnd,artvisc,compile=True)
Visualization of solution quantities¶
[9]:
gfu = GridFunction(fes)
gfh, gfhu, gfhv = gfu
gfvu = gfhu/gfh
gfvv = gfhv/gfh
momentum = CF((gfhu,gfhv))
velocity = CF((gfvu,gfvv))
gfu.Set(U0)
scenes = [ \
Draw(momentum,mesh,"mom"),
Draw(velocity,mesh,"vel"),
Draw(gfh,mesh,"h") ]
Explicit Euler time stepping¶
[10]:
def TimeLoop(a,gfu,dt,T,nsamplings=100,scenes=scenes,multidim_draw=False,md_nsamplings=20):
if multidim_draw:
gfu_t = GridFunction(gfu.space,multidim=True)
#gfu.Set(U0)
res = gfu.vec.CreateVector()
fes = a.space
t = 0; i = 0
nsteps = int(ceil(T/dt))
invma = fes.Mass(1).Inverse() @ a.mat
if multidim_draw:
gfu_t.AddMultiDimComponent(gfu.vec)
with TaskManager():
while t <= T - 0.5*dt:
res = invma * gfu.vec
gfu.vec.data -= dt * res
t += dt
if (i+1) % int(nsteps/nsamplings) == 0:
for s in scenes: s.Redraw()
if multidim_draw and (i+1) % int(nsteps/md_nsamplings) == 0:
gfu_t.AddMultiDimComponent(gfu.vec)
i+=1
print("\rt = {:.10}".format(t),end="")
for s in scenes: s.Redraw()
if multidim_draw:
return gfu_t
[11]:
gfu.Set(U0)
with TaskManager():
gfu_t = TimeLoop(a,gfu,dt=0.0025,T=15,multidim_draw=True,md_nsamplings=5)
t = 15.0
[12]:
Draw(gfu_t.components[0],mesh,"h",interpolate_multidim=True,animate=True,
deformation=True, settings = {"camera" :
{"transformations" :
[{ "type": "rotateX", "angle": -20},
{ "type": "rotateZ", "angle": 0}]}},
min=2, max=5, autoscale=False)
[12]:
BaseWebGuiScene
Tasks
You may play around with this example.
change the artificial diffusion parameter: How does it influence the solution
change boundary conditions: left boundary -> fixed height and non-reflecting
change the initial heights
introduce a (circular) obstacle below the dam
Generate output to create a video: To this end take a look at the final unit of this section.