This page was generated from unit-8.5-spacetime_unfitted/spacetime_unfitted.ipynb.

In this tutorial we make use of ipywidgets. You can (in the ideal case) simply install them with executing the next cell. You will however need to restart jupyter afterwards.

!pip3 install --user ipywidgets
!jupyter nbextension enable --py widgetsnbextension

Requirement already satisfied: ipywidgets in /usr/local/lib/python3.10/dist-packages (8.0.6)
Requirement already satisfied: ipython>=6.1.0 in /usr/local/lib/python3.10/dist-packages (from ipywidgets) (8.14.0)
Requirement already satisfied: ipykernel>=4.5.1 in /usr/local/lib/python3.10/dist-packages (from ipywidgets) (6.23.3)
Requirement already satisfied: traitlets>=4.3.1 in /usr/local/lib/python3.10/dist-packages (from ipywidgets) (5.9.0)
Requirement already satisfied: widgetsnbextension~=4.0.7 in /usr/local/lib/python3.10/dist-packages (from ipywidgets) (4.0.7)
Requirement already satisfied: jupyterlab-widgets~=3.0.7 in /usr/local/lib/python3.10/dist-packages (from ipywidgets) (3.0.7)
Requirement already satisfied: nest-asyncio in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (1.5.6)
Requirement already satisfied: debugpy>=1.6.5 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (1.6.7)
Requirement already satisfied: jupyter-client>=6.1.12 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (8.3.0)
Requirement already satisfied: psutil in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (5.9.5)
Requirement already satisfied: comm>=0.1.1 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (0.1.3)
Requirement already satisfied: matplotlib-inline>=0.1 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (0.1.6)
Requirement already satisfied: jupyter-core!=5.0.*,>=4.12 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (5.3.1)
Requirement already satisfied: packaging in /usr/lib/python3/dist-packages (from ipykernel>=4.5.1->ipywidgets) (21.3)
Requirement already satisfied: pyzmq>=20 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (25.1.0)
Requirement already satisfied: tornado>=6.1 in /usr/local/lib/python3.10/dist-packages (from ipykernel>=4.5.1->ipywidgets) (6.3.2)
Requirement already satisfied: backcall in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (0.2.0)
Requirement already satisfied: pygments>=2.4.0 in /usr/lib/python3/dist-packages (from ipython>=6.1.0->ipywidgets) (2.11.2)
Requirement already satisfied: decorator in /usr/lib/python3/dist-packages (from ipython>=6.1.0->ipywidgets) (4.4.2)
Requirement already satisfied: pexpect>4.3 in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (4.8.0)
Requirement already satisfied: stack-data in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (0.6.2)
Requirement already satisfied: prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30 in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (3.0.38)
Requirement already satisfied: jedi>=0.16 in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (0.18.2)
Requirement already satisfied: pickleshare in /usr/local/lib/python3.10/dist-packages (from ipython>=6.1.0->ipywidgets) (0.7.5)
Requirement already satisfied: parso<0.9.0,>=0.8.0 in /usr/local/lib/python3.10/dist-packages (from jedi>=0.16->ipython>=6.1.0->ipywidgets) (0.8.3)
Requirement already satisfied: python-dateutil>=2.8.2 in /usr/local/lib/python3.10/dist-packages (from jupyter-client>=6.1.12->ipykernel>=4.5.1->ipywidgets) (2.8.2)
Requirement already satisfied: platformdirs>=2.5 in /usr/local/lib/python3.10/dist-packages (from jupyter-core!=5.0.*,>=4.12->ipykernel>=4.5.1->ipywidgets) (3.8.0)
Requirement already satisfied: ptyprocess>=0.5 in /usr/local/lib/python3.10/dist-packages (from pexpect>4.3->ipython>=6.1.0->ipywidgets) (0.7.0)
Requirement already satisfied: wcwidth in /usr/local/lib/python3.10/dist-packages (from prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30->ipython>=6.1.0->ipywidgets) (0.2.6)
Requirement already satisfied: asttokens>=2.1.0 in /usr/local/lib/python3.10/dist-packages (from stack-data->ipython>=6.1.0->ipywidgets) (2.2.1)
Requirement already satisfied: pure-eval in /usr/local/lib/python3.10/dist-packages (from stack-data->ipython>=6.1.0->ipywidgets) (0.2.2)
Requirement already satisfied: executing>=1.2.0 in /usr/local/lib/python3.10/dist-packages (from stack-data->ipython>=6.1.0->ipywidgets) (1.2.0)
Requirement already satisfied: six in /usr/lib/python3/dist-packages (from asttokens>=2.1.0->stack-data->ipython>=6.1.0->ipywidgets) (1.16.0)
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv
Enabling notebook extension jupyter-js-widgets/extension...
      - Validating: OK

8.5 Space-time discretizations on unfitted geometries

In this example we consider a moving domain problem with homogeneous Neumann boundary conditions:

\[\begin{split}\left\{ \begin{aligned} \partial_t u + \mathbf{w} \cdot \nabla u - \alpha \Delta u &= f \quad \text{ in } \Omega(t), & \\ ~ \partial_{\mathbf{n}} u &= 0 \quad \text{ on } \partial \Omega(t), & \\ u &= u_0 \quad \text{at } t=0, & \\ \end{aligned}\right.\end{split}\]

\[\operatorname{div}(\mathbf{w}) = 0 \quad \text{ in } \Omega(t), \quad \mathbf{w} \cdot n = \mathcal{V}_n \text{ on } \partial \Omega(t).\]

We consider the Discountinuous Galerkin space-time discretization as discussed in [1, 2], which is of high order in space and time.

Literature:

from ngsolve import *
from netgen.geom2d import SplineGeometry
from xfem import *
from math import pi
from xfem.lset_spacetime import *
ngsglobals.msg_level = 1

#import netgen.gui
DrawDC = MakeDiscontinuousDraw(Draw)

importing ngsxfem-2.1.2301

Firstly, we pick some discretisation parameters:

# DISCRETIZATION PARAMETERS:

# Parameter for refinement study:
i = 3
n_steps = 2**i
space_refs = i

# Polynomial order in time
k_t = 2
# Polynomial order in space
k_s = k_t
# Polynomial order in time for level set approximation
lset_order_time = k_t
# Integration order in time
time_order = 2 * k_t
# Time stepping parameters
tstart = 0
tend = 0.5
delta_t = (tend - tstart) / n_steps
maxh = 0.5
# Ghost-penalty parameter
gamma = 0.05

Background geometry and mesh:

• We consider a simple square as background domain an use a simple mesh for that.

• The space-time method uses tensor-product elements. Hence, we do not need space-time meshes.

# Outer domain:
rect = SplineGeometry()
rect.AddRectangle([-0.6, -1], [0.6, 1])
ngmesh = rect.GenerateMesh(maxh=maxh, quad_dominated=False)
for j in range(space_refs):
    ngmesh.Refine()
mesh = Mesh(ngmesh)

 Generate Mesh from spline geometry

Handling of the time variable

For the handling of the space-time integration we use the following rules: * every time step is formulated with respect to the reference interval \([0,1)\) in time

• Example: \(t_{n-1} = 0.4\), \(t=0.55\), \(\Delta t = 0.2\) \(\quad \longrightarrow \quad\) \(\hat{t} = 0.75\).

• \(\hat{t}\) is the ReferenceTimeVariable (tref)

• We define \(t_{old}(=t_{n-1})\) and \(\Delta t\) as a Parameter, s.t. we can change the time interval later

# Map from reference time to physical time
told = Parameter(tstart)
t = told + delta_t * tref

Data functions (depending on \(t\))

# Level set geometry
# Radius of disk (the geometry)
R = 0.5
# Position shift of the geometry in time
rho = (1 / (pi)) * sin(2 * pi * t)
# Convection velocity:
w = CoefficientFunction((0, rho.Diff(t)))
# Level set
r = sqrt(x**2 + (y - rho)**2)
levelset = r - R

# Diffusion coefficient
alpha = 1
# Solution
u_exact = cos(pi * r / R) * sin(pi * t)
# R.h.s.
coeff_f = (u_exact.Diff(t)
           - alpha * (u_exact.Diff(x).Diff(x) + u_exact.Diff(y).Diff(y))
           + w[0] * u_exact.Diff(x) + w[1] * u_exact.Diff(y)).Compile()

Warning: differentiationg by a variable not marked as Variable,
might be optimized out. Call MakeVariable for differentiation CF
Warning: differentiationg by a variable not marked as Variable,
might be optimized out. Call MakeVariable for differentiation CF

A View on the time-dependent level set function

r_one_timestep = sqrt(x**2 + (y - (1 / (pi)) * sin(2 * pi * tref))**2)
levelset_one_timestep = r_one_timestep - R
TimeSlider_Draw(levelset_one_timestep,mesh,autoscale=False,min=-0.02,max=0.02,deformation=True)

<function xfem.TimeSlider_Draw.<locals>.UpdateTime(time)>

u_exact_one_timestep = cos(pi * r_one_timestep / R) * sin(pi * t)
TimeSlider_DrawDC(levelset_one_timestep,u_exact_one_timestep,0,mesh)

<function xfem.TimeSlider_DrawDC.<locals>.UpdateTime(time)>

Space-Time finite elements

• For the construction of a space-time FESpace we can combine any spatial FESpace with a scalar FiniteElement in a tensor-product fashion.

• Here, we use a nodal FiniteElement to simplify the extraction of spatial functions at fixed times.

# Spatial FESpace for solution
fes1 = H1(mesh, order=k_s, dgjumps=True)
# Time finite element (nodal!)
tfe = ScalarTimeFE(k_t)
# (Tensor product) space-time finite element space
st_fes = tfe * fes1

Levelset mesh adaptation class

• In order to achieve higher order accuracy in space, a variant of the isoparametric mapping introduced in 3 is applied.

Literature:

# Space time version of Levelset Mesh Adapation object. Also offers integrator
# helper functions that involve the correct mesh deformation
lsetadap = LevelSetMeshAdaptation_Spacetime(mesh, order_space=k_s,
                                            order_time=lset_order_time,
                                            threshold=0.5,
                                            discontinuous_qn=True)

The CutInfo class also works for space-time geometries. Its initialization is trivial:

ci = CutInfo(mesh, time_order=0)

Note the argument time_order=0 which makes the CutInfo looking for space-time cut information afterwards.

In addition, we define a Bitarray for the facets of the mesh for later use in the definition of the Ghost-penalty stabilisation.

ba_facets = BitArray(mesh.nfacet)
active_dofs = BitArray(st_fes.ndof)

To Update the slab geometry later on (for updated values of told) we do the following: * update of the isoparametric mapping * update of the cut information * update of facet markers * update of dof markers

def UpdateTimeSlabGeometry():
    lsetadap.CalcDeformation(levelset)

    # Update markers in (space-time) mesh
    ci.Update(lsetadap.levelsetp1[INTERVAL], time_order=0)

    # re-compute the facets for stabilization:
    ba_facets[:] = GetFacetsWithNeighborTypes(mesh,
                                              a=ci.GetElementsOfType(HASNEG),
                                              b=ci.GetElementsOfType(IF))
    active_dofs[:] = GetDofsOfElements(st_fes, ci.GetElementsOfType(HASNEG))

Note that here the call of CalcDeformation of lsetadap entails the calculation of the P1 projection of the levelset function internally. The space-time P1-in-space level set approximation of lsetadap can be accessed by lsetadap.levelsetp1[timetype] where timetype is either INTERVAL which yields the space-time function or TOP or BOTTOM which yields the spatial P1 function that is obtained by restriction to either tref=1 or tref=0. Similarly the access to the deformation is organized as lsetadap.deformation[timetype].

gfu = GridFunction(st_fes)
u_last = CreateTimeRestrictedGF(gfu, 1)
scene = DrawDC(lsetadap.levelsetp1[TOP], u_last, 0, mesh, "u_last",
               deformation=lsetadap.deformation[TOP])

Variational formulation

Now we would like to derive a suitable variational formulation on the time slabs \(Q^{n}\).

We start by multiplying the equation

\begin{equation*} \partial_{t} u- \alpha \Delta{u} + w \cdot \nabla{u} = f \quad in \quad \Omega(t), \qquad t \in [0,T] \end{equation*} by a test function \(v\) and perform integration by parts.

Due to homogeneous Neumann boundary conditions this leads to: \begin{equation*} (\partial_{t} u, v)_{Q^n} + \alpha (\nabla{u},\nabla{v})_{Q^n} + (w \cdot \nabla{u},v)_{Q^n} = (f,v)_{Q^n}. \end{equation*}

Upwind DG in time

In order to impose weak continuity in time, an upwind stabilisation is added, yielding

\begin{equation*} (\partial_{t} u, v)_{Q^n} + \alpha (\nabla{u},\nabla{v})_{Q^n} + (w \cdot \nabla{u},v)_{Q^n} + (u_{n−1}^+,v_{n−1}^+)_{\Omega^{n−1}} = (f,v)_{Q^n} + (u_{n−1}^-,v_{n−1}^+)_{\Omega^{n−1}}. \end{equation*}

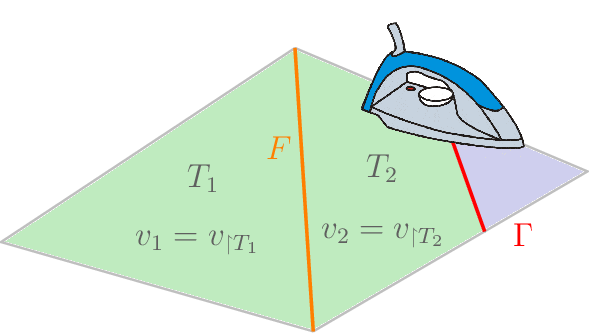
Ghost penalty stabilization

To gain sufficient control on all space-time d.o.f.s we add a so-called Ghost-Penalty stabilization as in [1]. Adding the stabilization, the variational formulation on the time slabs becomes:

:nbsphinx-math:`begin{alignat*}{3} begin{aligned}

&(partial_t u, v)_{Q^{n}} + alpha (nabla{u},nabla{v})_{Q^{n}} + (v, nabla{u} cdot w)_{Q^{n}} + (u_{n−1}^+,v_{n−1}^+)_{Omega^{n−1}} + s_h(u,v) \ &= (f,v)_{Q^{n}} + (u_{n−1}^-,v_{n−1}^+)_{Omega^{n−1}} \

end{aligned} end{alignat*}`

\[\begin{split}\text{with} \qquad\qquad s_h(u,v) = \sum\limits_{F \in F_{h}}{ \gamma_{j} \int\limits_{t_{n-1}}^{t_{n}}{ \int\limits_{\omega_F}{ h^{-2} [\![ u]\!] \, [\![ v]\!] \, d\mathbf{x} \, dt. } } } \\\end{split}\]

where \([\![u]\!]\) is the difference of \(u|_{T_1}\) and \(u|_{T_2}\) (interpreted as polynomials \(\in \mathbb{R}^d\)) and \(F_h\) is the set of facets on which the stabilization shall be applied.

Implementation of space-time integrals

u,v = st_fes.TnT()
h = specialcf.mesh_size

Transformation from reference interval to \((t_{n-1},t_n)\):

The transformation

\[(x,\hat{t}) \to (x,t_{n-1} + \hat{t} \Delta t), \qquad v(x,t) = \hat{v}(x,\hat{t}), \quad u(x,t) = \hat{u}(x,\hat{t}).\]

implies the following for the time derivative.

def dt(u):
    return 1.0 / delta_t * dtref(u)

Next, we define integration region symbols, which are the numerical counterparts of the regions introduced above. Note that the levelset deformation is included to achieve higher order in space. The definedonelements information is not necessary (for the first three symbols), but helpful for efficiency reasons.

dQ = delta_t * dCut(lsetadap.levelsetp1[INTERVAL], NEG, time_order=time_order,
                    deformation=lsetadap.deformation[INTERVAL],
                    definedonelements=ci.GetElementsOfType(HASNEG))
dOmold = dCut(lsetadap.levelsetp1[BOTTOM], NEG,
              deformation=lsetadap.deformation[BOTTOM],
              definedonelements=ci.GetElementsOfType(HASNEG), tref=0)
dOmnew = dCut(lsetadap.levelsetp1[TOP], NEG,
              deformation=lsetadap.deformation[TOP],
              definedonelements=ci.GetElementsOfType(HASNEG), tref=1)
dw = delta_t * dFacetPatch(definedonelements=ba_facets, time_order=time_order,
                           deformation=lsetadap.deformation[INTERVAL])

Now we setup the bilinear form and linear form corresponding to the previously described discrete variational formulation.

a = RestrictedBilinearForm(st_fes, "a", check_unused=False,
                           element_restriction=ci.GetElementsOfType(HASNEG),
                           facet_restriction=ba_facets)

First integral: $ (\partialt u, v){Q^{n}}$

a += v * (dt(u) - dt(lsetadap.deform) * grad(u)) * dQ

Note that here, due to the time-dependent mesh deformation, the partial derivative in physical coordinates that we used in the formulation before corresponds to the partial derivative w.r.t. the reference configuration minus an additional mesh velocity contribution.

Second integral: \(\alpha (\nabla{u},\nabla{v})_{Q^{n}}\)

a += alpha * InnerProduct(grad(u), grad(v)) * dQ

Third integral: \((v, \nabla{u} \cdot w)_{Q^{n}}\)

a += v * w * grad(u) * dQ

Fourth integral: \((u_{n−1}^+,v_{n−1}^+)_{\Omega^{n−1}}\)

a += u * v * dOmold

Fifth integral:

\[s_h(u,v) = \sum\limits_{F \in F_{h}}{ \gamma_{j} \int\limits_{t_{n-1}}^{t_{n}}{ \int\limits_{\omega_F}{ h^{-2} [\![ u]\!] \, [\![ v]\!] \, d\mathbf{x} \, dt. }}} = \sum\limits_{F \in F_{h}}{ \Delta t \ \gamma_{j} \int\limits_{t_{n-1}}^{t_{n}}{ \int\limits_{\omega_F}{ h^{-2} [\![ \hat u]\!] \, [\![ \hat v]\!] \, d\mathbf{x} \, dt. }}}\]

a += h**(-2) * (1 + delta_t / h) * gamma * \
    (u - u.Other()) * (v - v.Other()) * dw

Sixth integral: \((f,v)_{Q^{n}}\)

f = LinearForm(st_fes)
f += coeff_f * v * dQ

Seventh integral: \((u_{n−1}^-,v_{n−1}^+)_{\Omega^{n−1}}\)

f += u_last * v * dOmold

• setup the new linear system

• solve the linear system

def SolveForTimeSlab():
    a.Assemble(reallocate=True)
    f.Assemble()
    inv = a.mat.Inverse(active_dofs, inverse="umfpack")
    gfu.vec.data = inv * f.vec.data

• store the solution at \(t_n\) into a (purely) spatial GridFunction (to be used in next time step)

• compute the error

• update visualization

def FinalizeStep(scene=None):
    # Evaluate upper trace of solution for
    #  * for error evaluation
    #  * upwind-coupling to next time slab
    RestrictGFInTime(spacetime_gf=gfu, reference_time=1.0, space_gf=u_last)

    # Compute error at final time
    l2error = sqrt(Integrate((u_exact - u_last)**2 * dOmnew, mesh))
    print("\rt = {0:12.9f}, L2 error = {1:12.9e}".format(told.Get(), l2error), end="")
    if scene:
        scene.Redraw()

scene = DrawDC(lsetadap.levelsetp1[TOP],u_last,-2, mesh,"u", autoscale=False, min = -2, max = 1, deformation = lsetadap.deformation[TOP])

Due to the mesh deformation changing (discontinuously) between time slabs, we have to project solutions from one time slab to the other. This is automatically done for all GridFunctions registered in lsetadap by ProjectOnUpdate.

# Set initial values
u_last.Set(fix_tref(u_exact, 0))
# Project u_last at the beginning of each time step
lsetadap.ProjectOnUpdate(u_last)
told.Set(0)
with TaskManager():
    while tend - told.Get() > delta_t/2:
        UpdateTimeSlabGeometry()
        SolveForTimeSlab()
        told.Set(told.Get() + delta_t)
        FinalizeStep(scene)
print("")

t =  0.500000000, L2 error = 3.273189062e-01

Play around suggestions:

• use other orders in space or time (and a coarse grid)

• use different level set evolutions

Further material:

Take a look at the demos in demos/spacetime of the ngsxfem repository.