This page was generated from unit-2.3-hcurlhdiv/hcurlhdiv.ipynb.

2.3 H(curl) and H(div) function spaces

Scalar and vectorial finite elements in NGSolve:

Standard continuous \(H^1\) elements: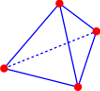

Nedelec’s tangentially-continuous \(H(curl)\)-conforming edge elements:

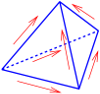
Raviart-Thomas normally-continuous \(H(div)\)-conforming face elements:

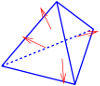
Discontinuous \(L_2\) elements:

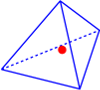
These vector-valued spaces allow to represent physical quantities which are either normally or tangentially continuous.

The finite element spaces are related by the de Rham complex:

\[\begin{split}\DeclareMathOperator{\Grad}{grad} \DeclareMathOperator{\Curl}{curl} \DeclareMathOperator{\Div}{div} \begin{array}{ccccccc} H^1 & \stackrel{\Grad}{\longrightarrow} & H(\Curl) & \stackrel{\Curl}{\longrightarrow} & H(\Div) & \stackrel{\Div}{\longrightarrow} & L^2 \\[8pt] \bigcup & & \bigcup & & \bigcup & & \bigcup \\[8pt] W_{h} & \stackrel{\Grad}{\longrightarrow} & V_{h } & \stackrel{\Curl}{\longrightarrow} & Q_{h} & \stackrel{\Div}{\longrightarrow} & S_{h} \: \\[3ex] \end{array}\end{split}\]

NGSolve supports these elements of arbitrary order, on all common element shapes (trigs, quads, tets, prisms, pyramids, hexes). Elements may be curved.

from ngsolve import *
from ngsolve.webgui import Draw
from netgen.geom2d import unit_square
from netgen.csg import unit_cube
mesh = Mesh(unit_square.GenerateMesh(maxh=0.3))

 Generate Mesh from spline geometry
 Boundary mesh done, np = 12
 CalcLocalH: 12 Points 0 Elements 0 Surface Elements
 Meshing domain 1 / 1
 load internal triangle rules
 Surface meshing done
 Edgeswapping, topological
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Update mesh topology
 Update clusters

Generate a higher order \(H^1\)-space. We first explore its different types of basis functions.

order=3
fes = H1(mesh, order=order)
gfu = GridFunction(fes)
Draw(gfu)

BaseWebGuiScene

The first basis functions are hat-functions, one per vertex. By setting the solution vector to a unit-vector, we may look at the individual basis functions:

gfu.vec[:] = 0
# vertex nr:
gfu.vec[17] = 1
Draw(gfu, min=0, max=1, deformation=True)

BaseWebGuiScene

The next are edge-bubbles, where we have \((p-1)\) basis functions per edge. A NodeId object refers to a particular vertex, edge, face or cell node in the mesh. We can ask for the degrees of freedom on a node:

# basis functions on edge nr:
edge_dofs = fes.GetDofNrs(NodeId(EDGE,10))
print("edge_dofs =", edge_dofs)
gfu.vec[:] = 0
gfu.vec[edge_dofs[0]] = 1
Draw(gfu, order=3, min=-0.05, max=0.05, deformation=True)

edge_dofs = (39, 40)

BaseWebGuiScene

Finally, we have \((p-1)(p-2)/2\) inner basis functions on every triangle:

trig_dofs = fes.GetDofNrs(NodeId(FACE,0))
print("trig_dofs = ", trig_dofs)
gfu.vec[:] = 0
gfu.vec[trig_dofs[0]] = 1
Draw(gfu, order=3, min=0, max=0.03, deformation=True)

trig_dofs =  (103,)

BaseWebGuiScene

The FESpace also maintains information about local dofs, interface dofs and wire-basket dofs for the BDDC preconditioner:

for i in range(fes.ndof):
    print (i,":", fes.CouplingType(i))

0 : COUPLING_TYPE.WIREBASKET_DOF
1 : COUPLING_TYPE.WIREBASKET_DOF
2 : COUPLING_TYPE.WIREBASKET_DOF
3 : COUPLING_TYPE.WIREBASKET_DOF
4 : COUPLING_TYPE.WIREBASKET_DOF
5 : COUPLING_TYPE.WIREBASKET_DOF
6 : COUPLING_TYPE.WIREBASKET_DOF
7 : COUPLING_TYPE.WIREBASKET_DOF
8 : COUPLING_TYPE.WIREBASKET_DOF
9 : COUPLING_TYPE.WIREBASKET_DOF
10 : COUPLING_TYPE.WIREBASKET_DOF
11 : COUPLING_TYPE.WIREBASKET_DOF
12 : COUPLING_TYPE.WIREBASKET_DOF
13 : COUPLING_TYPE.WIREBASKET_DOF
14 : COUPLING_TYPE.WIREBASKET_DOF
15 : COUPLING_TYPE.WIREBASKET_DOF
16 : COUPLING_TYPE.WIREBASKET_DOF
17 : COUPLING_TYPE.WIREBASKET_DOF
18 : COUPLING_TYPE.WIREBASKET_DOF
19 : COUPLING_TYPE.INTERFACE_DOF
20 : COUPLING_TYPE.INTERFACE_DOF
21 : COUPLING_TYPE.INTERFACE_DOF
22 : COUPLING_TYPE.INTERFACE_DOF
23 : COUPLING_TYPE.INTERFACE_DOF
24 : COUPLING_TYPE.INTERFACE_DOF
25 : COUPLING_TYPE.INTERFACE_DOF
26 : COUPLING_TYPE.INTERFACE_DOF
27 : COUPLING_TYPE.INTERFACE_DOF
28 : COUPLING_TYPE.INTERFACE_DOF
29 : COUPLING_TYPE.INTERFACE_DOF
30 : COUPLING_TYPE.INTERFACE_DOF
31 : COUPLING_TYPE.INTERFACE_DOF
32 : COUPLING_TYPE.INTERFACE_DOF
33 : COUPLING_TYPE.INTERFACE_DOF
34 : COUPLING_TYPE.INTERFACE_DOF
35 : COUPLING_TYPE.INTERFACE_DOF
36 : COUPLING_TYPE.INTERFACE_DOF
37 : COUPLING_TYPE.INTERFACE_DOF
38 : COUPLING_TYPE.INTERFACE_DOF
39 : COUPLING_TYPE.INTERFACE_DOF
40 : COUPLING_TYPE.INTERFACE_DOF
41 : COUPLING_TYPE.INTERFACE_DOF
42 : COUPLING_TYPE.INTERFACE_DOF
43 : COUPLING_TYPE.INTERFACE_DOF
44 : COUPLING_TYPE.INTERFACE_DOF
45 : COUPLING_TYPE.INTERFACE_DOF
46 : COUPLING_TYPE.INTERFACE_DOF
47 : COUPLING_TYPE.INTERFACE_DOF
48 : COUPLING_TYPE.INTERFACE_DOF
49 : COUPLING_TYPE.INTERFACE_DOF
50 : COUPLING_TYPE.INTERFACE_DOF
51 : COUPLING_TYPE.INTERFACE_DOF
52 : COUPLING_TYPE.INTERFACE_DOF
53 : COUPLING_TYPE.INTERFACE_DOF
54 : COUPLING_TYPE.INTERFACE_DOF
55 : COUPLING_TYPE.INTERFACE_DOF
56 : COUPLING_TYPE.INTERFACE_DOF
57 : COUPLING_TYPE.INTERFACE_DOF
58 : COUPLING_TYPE.INTERFACE_DOF
59 : COUPLING_TYPE.INTERFACE_DOF
60 : COUPLING_TYPE.INTERFACE_DOF
61 : COUPLING_TYPE.INTERFACE_DOF
62 : COUPLING_TYPE.INTERFACE_DOF
63 : COUPLING_TYPE.INTERFACE_DOF
64 : COUPLING_TYPE.INTERFACE_DOF
65 : COUPLING_TYPE.INTERFACE_DOF
66 : COUPLING_TYPE.INTERFACE_DOF
67 : COUPLING_TYPE.INTERFACE_DOF
68 : COUPLING_TYPE.INTERFACE_DOF
69 : COUPLING_TYPE.INTERFACE_DOF
70 : COUPLING_TYPE.INTERFACE_DOF
71 : COUPLING_TYPE.INTERFACE_DOF
72 : COUPLING_TYPE.INTERFACE_DOF
73 : COUPLING_TYPE.INTERFACE_DOF
74 : COUPLING_TYPE.INTERFACE_DOF
75 : COUPLING_TYPE.INTERFACE_DOF
76 : COUPLING_TYPE.INTERFACE_DOF
77 : COUPLING_TYPE.INTERFACE_DOF
78 : COUPLING_TYPE.INTERFACE_DOF
79 : COUPLING_TYPE.INTERFACE_DOF
80 : COUPLING_TYPE.INTERFACE_DOF
81 : COUPLING_TYPE.INTERFACE_DOF
82 : COUPLING_TYPE.INTERFACE_DOF
83 : COUPLING_TYPE.INTERFACE_DOF
84 : COUPLING_TYPE.INTERFACE_DOF
85 : COUPLING_TYPE.INTERFACE_DOF
86 : COUPLING_TYPE.INTERFACE_DOF
87 : COUPLING_TYPE.INTERFACE_DOF
88 : COUPLING_TYPE.INTERFACE_DOF
89 : COUPLING_TYPE.INTERFACE_DOF
90 : COUPLING_TYPE.INTERFACE_DOF
91 : COUPLING_TYPE.INTERFACE_DOF
92 : COUPLING_TYPE.INTERFACE_DOF
93 : COUPLING_TYPE.INTERFACE_DOF
94 : COUPLING_TYPE.INTERFACE_DOF
95 : COUPLING_TYPE.INTERFACE_DOF
96 : COUPLING_TYPE.INTERFACE_DOF
97 : COUPLING_TYPE.INTERFACE_DOF
98 : COUPLING_TYPE.INTERFACE_DOF
99 : COUPLING_TYPE.INTERFACE_DOF
100 : COUPLING_TYPE.INTERFACE_DOF
101 : COUPLING_TYPE.INTERFACE_DOF
102 : COUPLING_TYPE.INTERFACE_DOF
103 : COUPLING_TYPE.LOCAL_DOF
104 : COUPLING_TYPE.LOCAL_DOF
105 : COUPLING_TYPE.LOCAL_DOF
106 : COUPLING_TYPE.LOCAL_DOF
107 : COUPLING_TYPE.LOCAL_DOF
108 : COUPLING_TYPE.LOCAL_DOF
109 : COUPLING_TYPE.LOCAL_DOF
110 : COUPLING_TYPE.LOCAL_DOF
111 : COUPLING_TYPE.LOCAL_DOF
112 : COUPLING_TYPE.LOCAL_DOF
113 : COUPLING_TYPE.LOCAL_DOF
114 : COUPLING_TYPE.LOCAL_DOF
115 : COUPLING_TYPE.LOCAL_DOF
116 : COUPLING_TYPE.LOCAL_DOF
117 : COUPLING_TYPE.LOCAL_DOF
118 : COUPLING_TYPE.LOCAL_DOF
119 : COUPLING_TYPE.LOCAL_DOF
120 : COUPLING_TYPE.LOCAL_DOF
121 : COUPLING_TYPE.LOCAL_DOF
122 : COUPLING_TYPE.LOCAL_DOF
123 : COUPLING_TYPE.LOCAL_DOF
124 : COUPLING_TYPE.LOCAL_DOF
125 : COUPLING_TYPE.LOCAL_DOF
126 : COUPLING_TYPE.LOCAL_DOF

\(H(curl)\) finite element space

In NGSolve we use hierarchical high order finite element basis functions with node-wise exact sequences. The lowest order space \(W_{l.o}\) is the edge-element space:

\[\begin{split}\begin{array}{rcll} W_{hp} & = & W_{p=1} + \sum_E W_E + \sum_F W_F + \sum_C W_C & \subset H^1 \\[0.5em] V_{hp} & = & W_{l.o} + \sum_E V_E + \sum_F V_F + \sum_C V_C & \subset H(curl) \end{array}\end{split}\]

where the edge, face and cell blocks are compatible in the sense that

\[\nabla W_E = V_E, \quad \nabla W_F \subset V_F, \quad \nabla W_C \subset V_C\]

We obtain this by using gradients of \(H^1\) basis functions as \(H(curl)\) basis functions, and some more (see thesis Sabine Zaglmayr):

\[\begin{split}\begin{array}{rcl} V_E & = & \text{span} \{ \nabla \varphi_{E,i}^{H^1} \} \\ V_F & = & \text{span} \{ \nabla \varphi_{F,i}^{H^1} \cup \widetilde \varphi_{F,i}^{H(curl)} \} \\ V_C & = & \text{span} \{ \nabla \varphi_{C,i}^{H^1} \cup \widetilde \varphi_{C,i}^{H(curl)} \} \end{array}\end{split}\]

fes = HCurl(mesh, order=2)
uc = GridFunction(fes, name="uc")

edge_dofs = fes.GetDofNrs(NodeId(EDGE,10))
print ("edgedofs: ", edge_dofs)
uc.vec[:] = 0
uc.vec[edge_dofs[0]] = 1
Draw (uc, min=0, max=3)
Draw (curl(uc), mesh, "curl", min=0, max=3)
Draw (Norm(uc), mesh, "norm-uc", min=0, max=3)

edgedofs:  (10, 62, 63)

BaseWebGuiScene

look at them by activating Draw Surface Vectors.

face_dofs = fes.GetDofNrs(NodeId(FACE,10))
print ("facedofs: ", face_dofs)
uc.vec[:] = 0
uc.vec[face_dofs[0]] = 1
Draw (uc, min=0, max=1)
Draw (curl(uc), mesh, "curl", min=0, max=1)
Draw (Norm(uc), mesh, "norm-uc", min=0, max=1)

facedofs:  (144, 145, 146)

BaseWebGuiScene

\(H(div)\) finite element space

NGSolve provides Raviart-Thomas (RT) as well as Brezzi-Douglas-Marini (BDM) finite element spaces for H(div). We obtain the RT-version by setting RT=True

fes = HDiv(mesh, order=2, RT=True)
ud = GridFunction(fes, name="ud")
func = x*y*(x,y)
ud.Set (func)
Draw (ud)
print ("interpolation error:", Integrate ((func-ud)**2, mesh))

setvalues element 24/24

interpolation error: 2.2998491803729166e-31

The function spaces know their canonical derivatives. These operations are efficiently implemented by transformation from the reference element.

gfu.derivname, ud.derivname, uc.derivname

('grad', 'div', 'curl')

But there are additional options, like forming the element-wise gradient of H(div) finite element functions. We can query the available operators via

print ("H(div) operators: ", ud.Operators())

H(div) operators:  ['grad', 'dual', 'normalcomponent']

and access them via the Operator() method

Draw (grad(ud)[0,1], mesh, "gradud")

BaseWebGuiScene