This page was generated from unit-2.1.3-bddc/bddc.ipynb.

2.1.3 Element-wise BDDC Preconditioner¶

The element-wise BDDC (Balancing Domain Decomposition preconditioner with Constraints) preconditioner in NGSolve is a good general purpose preconditioner that works well both in the shared memory parallel mode as well as in distributed memory mode. In this tutorial, we discuss this preconditioner, related built-in options, and customization from python.

Let us start with a simple description of the element-wise BDDC in the context of Lagrange finite element space \(V\). Here the BDDC preconditoner is constructed on an auxiliary space \(\widetilde{V}\) obtained by connecting only element vertices (leaving edge and face shape functions discontinuous). Although larger, the auxiliary space allows local elimination of edge and face variables. Hence an analogue of the original matrix \(A\) on this space, named \(\widetilde A\), is less expensive to invert. This inverse is used to construct a preconditioner for \(A\) as follows:

\[C_{BDDC}^{-1} = R {\,\widetilde{A}\,}^{-1}\, R^t\]

Here, \(R\) is the averaging operator for the discontinous edge and face variables.

To construct a general purpose BDDC preconditioner, NGSolve generalizes this idea to all its finite element spaces by a classification of degrees of freedom. Dofs are classified into (condensable) LOCAL_DOFs that we saw in 1.4 and a remainder that includes these types:

WIREBASKET_DOF

INTERFACE_DOF

The original finite element space \(V\) is obtained by requiring conformity of both the above types of dofs, while the auxiliary space \(\widetilde{V}\) is obtained by requiring conformity of WIREBASKET_DOFs only.

Here is a figure of a typical function in the default \(\widetilde{V}\) (and the code to generate this is at the end of this tutorial) when \(V\) is the Lagrange space:

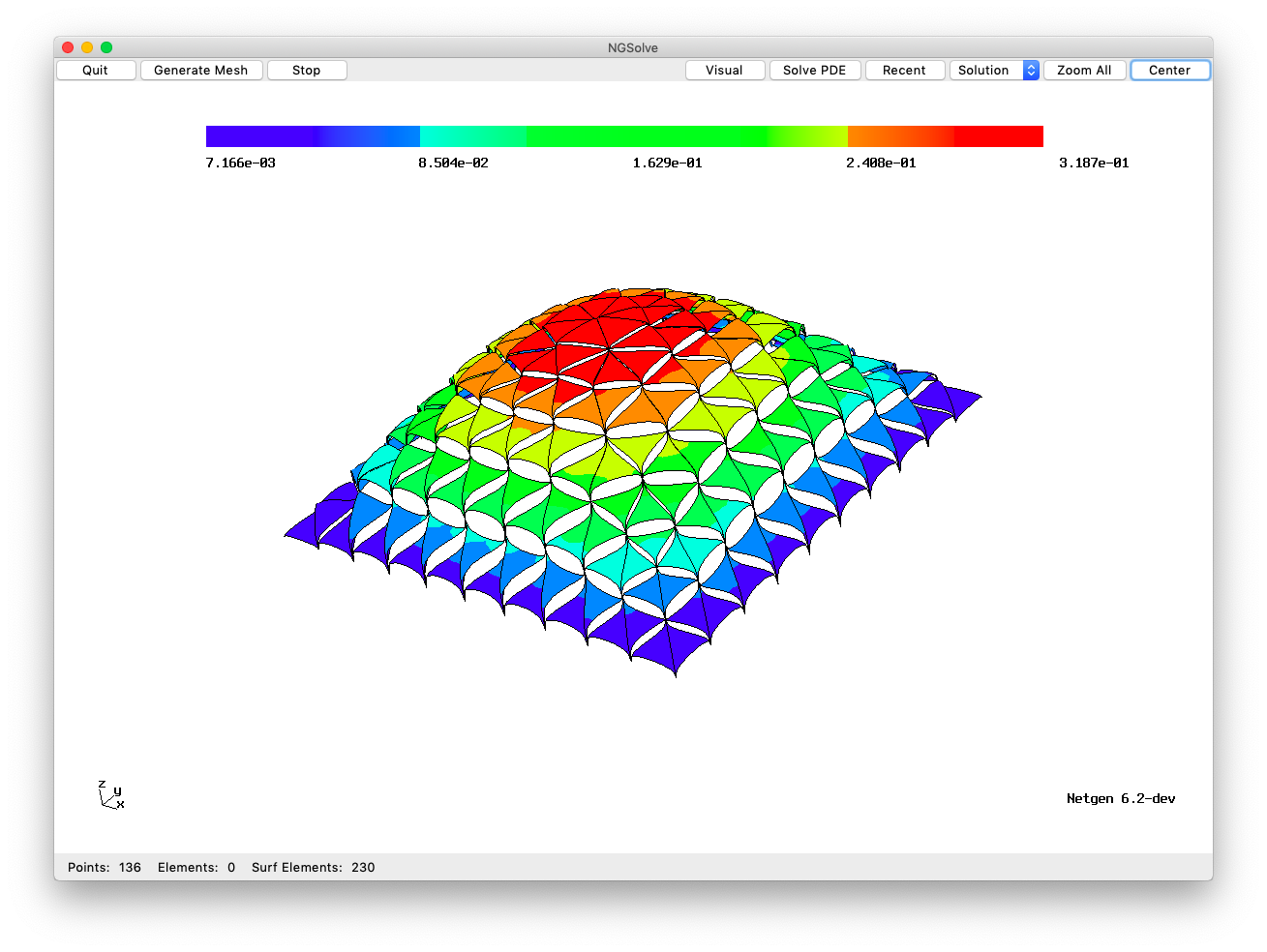
title

[1]:

from ngsolve import *
from ngsolve.webgui import Draw
from ngsolve.la import EigenValues_Preconditioner
from netgen.csg import unit_cube
from netgen.geom2d import unit_square
SetHeapSize(100*1000*1000)

[2]:

mesh = Mesh(unit_cube.GenerateMesh(maxh=0.5))
# mesh = Mesh(unit_square.GenerateMesh(maxh=0.5))

 Start Findpoints
 main-solids: 1
 Found points 8
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 CalcLocalH: 20 Points 0 Elements 0 Surface Elements
 Start Findpoints
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 Start Findpoints
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 Surface 1 / 6
 load internal triangle rules
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 Surface 2 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 Surface 3 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 Surface 4 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 Surface 5 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 Surface 6 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 6 elements, 20 points
 SplitSeparateFaces
 Check subdomain 1 / 1

 Meshing subdomain 1 of 1
 Use internal rules
 Delaunay meshing
 number of points: 20
 blockfill local h
 number of points: 29
 Points: 29
 Elements: 142
 Tree data entries per element: 1.40845
 Tree nodes per element: 0.0211268
 SwapImprove
 SwapImprove
 SwapImprove
 SwapImprove
 0 degenerated elements removed
 Remove intersecting
 Remove outer
 29 points, 64 elements
 start tetmeshing
 Use internal rules
 Success !
 29 points, 83 elements
 Remove Illegal Elements
 Volume Optimization
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 Update mesh topology
 Update clusters

Built-in options¶

Let us define a simple function to study how the spectrum of the preconditioned matrix changes with various options.

Effect of condensation¶

[3]:

def TestPreconditioner (p, condense=False, **args):
    fes = H1(mesh, order=p, **args)
    u,v = fes.TnT()
    a = BilinearForm(fes, eliminate_internal=condense)
    a += grad(u)*grad(v)*dx + u*v*dx
    c = Preconditioner(a, "bddc")
    a.Assemble()
    return EigenValues_Preconditioner(a.mat, c.mat)

[4]:

lams = TestPreconditioner(5)
print (lams[0:3], "...\n", lams[-3:])

assemble VOL element 63/63
call wirebasket inverse ( with 136 free dofs out of 1576 )
has inverse
 1.00228
  1.0408
 1.13959
 ...
  7.43053
 7.57517
 7.66553

eigen-it 0/200
eigen-it 1/200
eigen-it 2/200
eigen-it 3/200
eigen-it 4/200
eigen-it 5/200
eigen-it 6/200
eigen-it 7/200
eigen-it 8/200
eigen-it 9/200
eigen-it 10/200
eigen-it 11/200
eigen-it 12/200
eigen-it 13/200
eigen-it 14/200
eigen-it 15/200
eigen-it 16/200
eigen-it 17/200
eigen-it 18/200
eigen-it 19/200
eigen-it 20/200
eigen-it 21/200
eigen-it 22/200
eigen-it 23/200
eigen-it 24/200

Here is the effect of static condensation on the BDDC preconditioner.

[5]:

lams = TestPreconditioner(5, condense=True)
print (lams[0:3], "...\n", lams[-3:])

assemble VOL element 63/63
call wirebasket inverse ( with 136 free dofs out of 1576 )
has inverse
 1.00137
 1.03997
 1.11644
 ...
  6.92348
 7.01741
 7.29845
eigen-it 0/200
eigen-it 1/200
eigen-it 2/200
eigen-it 3/200
eigen-it 4/200
eigen-it 5/200
eigen-it 6/200
eigen-it 7/200
eigen-it 8/200
eigen-it 9/200
eigen-it 10/200
eigen-it 11/200
eigen-it 12/200
eigen-it 13/200
eigen-it 14/200
eigen-it 15/200
eigen-it 16/200
eigen-it 17/200
eigen-it 18/200
eigen-it 19/200
eigen-it 20/200
eigen-it 21/200
eigen-it 22/200
eigen-it 23/200

Tuning the auxiliary space¶

Next, let us study the effect of a few built-in flags for finite element spaces that are useful for tweaking the behavior of the BDDC preconditioner. The effect of these flags varies in two (2D) and three dimensions (3D), e.g.,

wb_fulledges=True: This option keeps all edge-dofs conforming (i.e. they are marked WIREBASKET_DOFs). This option is only meaningful in 3D. If used in 2D, the preconditioner becomes a direct solver.
wb_withedges=True: This option keeps only the first edge-dof conforming (i.e., the first edge-dof is marked WIREBASKET_DOF and the remaining edge-dofs are marked INTERFACE_DOFs).

The complete situation is a bit more complex due to the fact these options can take the three values True, False, or Undefined, the two options can be combined, and the space dimension can be 2 or 3. The default value of these flags in NGSolve is Undefined. Here is a table with the summary of the effect of these options:

wb_fulledges	wb_withedges	2D	3D
True	any value	all	all
False/Undefined	Undefined	none	first
False/Undefined	False	none	none
False/Undefined	True	first	first

An entry \(X \in\) {all, none, first} of the last two columns is to be read as follows: \(X\) of the edge-dofs is(are) WIREBASKET_DOF(s).

Here is an example of the effect of one of these flag values.

[6]:

lams = TestPreconditioner(5, condense=True,
                          wb_withedges=False)
print (lams[0:3], "...\n", lams[-3:])

assemble VOL element 63/63
call wirebasket inverse ( with 28 free dofs out of 1576 )
has inverse
 1.00412
 1.09464
 1.33392
 ...
  31.0804
 33.0369
 33.6461

eigen-it 0/200
eigen-it 1/200
eigen-it 2/200
eigen-it 3/200
eigen-it 4/200
eigen-it 5/200
eigen-it 6/200
eigen-it 7/200
eigen-it 8/200
eigen-it 9/200
eigen-it 10/200
eigen-it 11/200
eigen-it 12/200
eigen-it 13/200
eigen-it 14/200
eigen-it 15/200
eigen-it 16/200
eigen-it 17/200
eigen-it 18/200
eigen-it 19/200
eigen-it 20/200
eigen-it 21/200
eigen-it 22/200
eigen-it 23/200
eigen-it 24/200
eigen-it 25/200
eigen-it 26/200
eigen-it 27/200
eigen-it 28/200
eigen-it 29/200
eigen-it 30/200
eigen-it 31/200

Clearly, when moving from the default case (where the first of the edge dofs are wire basket dofs) to the case (where none of the edge dofs are wire basket dofs), the conditioning became less favorable.

Customize¶

From within python, we can change the types of degrees of freedom of finite element spaces, thus affecting the behavior of the BDDC preconditioner.

To depart from the default and commit the first two edge dofs to wire basket, we perform the next steps:

[7]:

fes = H1(mesh, order=10)
u,v = fes.TnT()

for ed in mesh.edges:
    dofs = fes.GetDofNrs(ed)
    for d in dofs:
        fes.SetCouplingType(d, COUPLING_TYPE.INTERFACE_DOF)

    # Set the first two edge dofs to be conforming
    fes.SetCouplingType(dofs[0], COUPLING_TYPE.WIREBASKET_DOF)
    fes.SetCouplingType(dofs[1], COUPLING_TYPE.WIREBASKET_DOF)

a = BilinearForm(fes, eliminate_internal=True)
a += grad(u)*grad(v)*dx + u*v*dx
c = Preconditioner(a, "bddc")
a.Assemble()

lams=EigenValues_Preconditioner(a.mat, c.mat)
max(lams)/min(lams)

assemble VOL element 63/63
call wirebasket inverse ( with 244 free dofs out of 11476 )
has inverse
eigen-it 0/200
eigen-it 1/200
eigen-it 2/200
eigen-it 3/200
eigen-it 4/200
eigen-it 5/200
eigen-it 6/200
eigen-it 7/200
eigen-it 8/200
eigen-it 9/200
eigen-it 10/200
eigen-it 11/200
eigen-it 12/200
eigen-it 13/200
eigen-it 14/200
eigen-it 15/200
eigen-it 16/200
eigen-it 17/200
eigen-it 18/200
eigen-it 19/200
eigen-it 20/200
eigen-it 21/200
eigen-it 22/200
eigen-it 23/200
eigen-it 24/200
eigen-it 25/200
eigen-it 26/200
eigen-it 27/200
eigen-it 28/200
eigen-it 29/200

[7]:

18.178677170664105

This is a slight improvement from the default.

[8]:

lams = TestPreconditioner (10, condense=True)
max(lams)/min(lams)

assemble VOL element 63/63
call wirebasket inverse ( with 136 free dofs out of 11476 )
has inverse

[8]:

27.35966282226837

eigen-it 0/200
eigen-it 1/200
eigen-it 2/200
eigen-it 3/200
eigen-it 4/200
eigen-it 5/200
eigen-it 6/200
eigen-it 7/200
eigen-it 8/200
eigen-it 9/200
eigen-it 10/200
eigen-it 11/200
eigen-it 12/200
eigen-it 13/200
eigen-it 14/200
eigen-it 15/200
eigen-it 16/200
eigen-it 17/200
eigen-it 18/200
eigen-it 19/200
eigen-it 20/200
eigen-it 21/200
eigen-it 22/200
eigen-it 23/200
eigen-it 24/200
eigen-it 25/200
eigen-it 26/200
eigen-it 27/200
eigen-it 28/200
eigen-it 29/200
eigen-it 30/200

Combine BDDC with AMG for large problems¶

The coarse inverse \({\,\widetilde{A}\,}^{-1}\) of BDDC is expensive on fine meshes. Using the option coarsetype=h1amg flag, we can ask BDDC to replace \({\,\widetilde{A}\,}^{-1}\) by an Algebraic MultiGrid (AMG) preconditioner. Since NGSolve’s h1amg is well-suited

for the lowest order Lagrange space, we use the option wb_withedges=False to ensure that \(\widetilde{A}\) is made solely with vertex unknowns.

[9]:

p = 5
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.05))
fes = H1(mesh, order=p, dirichlet="left|bottom|back",
         wb_withedges=False)
print("NDOF = ", fes.ndof)
u,v = fes.TnT()
a = BilinearForm(fes)
a += grad(u)*grad(v)*dx
f = LinearForm(fes)
f += v*dx

with TaskManager():
    pre = Preconditioner(a, "bddc", coarsetype="h1amg")
    a.Assemble()
    f.Assemble()

    gfu = GridFunction(fes)
    solvers.CG(mat=a.mat, rhs=f.vec, sol=gfu.vec,
               pre=pre, maxsteps=500)
Draw(gfu)

 Start Findpoints
 main-solids: 1
 Found points 8
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 CalcLocalH: 236 Points 0 Elements 0 Surface Elements
 Start Findpoints
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 Start Findpoints
 Analyze spec points
 Find edges
 12 edges found
 Check intersecting edges
 Surface 1 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 922 elements, 658 points
 Surface 2 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 964 elements, 1101 points
 Surface 3 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 970 elements, 1547 points
 Surface 4 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 946 elements, 1981 points
 Surface 5 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 970 elements, 2427 points
 Surface 6 / 6
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 970 elements, 2873 points
 SplitSeparateFaces
 Check subdomain 1 / 1

 Meshing subdomain 1 of 1
 Use internal rules
 Delaunay meshing
 number of points: 2827
 blockfill local h
 number of points: 12268
 Points: 12268
 Elements: 71430
 Tree data entries per element: 1.69537
 Tree nodes per element: 0.0338933
 SwapImprove
 SwapImprove
 SwapImprove
 SwapImprove
 0 degenerated elements removed
 Remove intersecting
 Remove outer
 12268 points, 65567 elements
 start tetmeshing
 Use internal rules
 Success !
 12268 points, 65567 elements
 Remove Illegal Elements
 Volume Optimization
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 CombineImprove
 ImproveMesh
 SplitImprove
 ImproveMesh
 SwapImprove
 SwapImprove2
 ImproveMesh
 Update mesh topology
NDOF =  1170736
 Update clusters

WARNING: kwarg 'coarsetype' is an undocumented flags option for class <class 'ngsolve.comp.Preconditioner'>, maybe there is a typo?

Create H1AMG
assemble VOL element 54420/54420
call wirebasket preconditioner finalize ( with 9346 free dofs out of 1170736 )
H1AMG: level = 0, num_edges = 58513, nv = 1170736
BlockJacobi Preconditioner, constructor called, #blocks = 4842
BlockJacobi Preconditioner built
H1AMG: level = 1, num_edges = 30950, nv = 4842
BlockJacobi Preconditioner, constructor called, #blocks = 2529
BlockJacobi Preconditioner built
H1AMG: level = 2, num_edges = 16576, nv = 2529
BlockJacobi Preconditioner, constructor called, #blocks = 1328
BlockJacobi Preconditioner built
H1AMG: level = 3, num_edges = 8692, nv = 1328
BlockJacobi Preconditioner, constructor called, #blocks = 696
BlockJacobi Preconditioner built
H1AMG: level = 4, num_edges = 4505, nv = 696
BlockJacobi Preconditioner, constructor called, #blocks = 369
BlockJacobi Preconditioner built
H1AMG: level = 5, num_edges = 2311, nv = 369
BlockJacobi Preconditioner, constructor called, #blocks = 192
BlockJacobi Preconditioner built
H1AMG: level = 6, num_edges = 1133, nv = 192
BlockJacobi Preconditioner, constructor called, #blocks = 100
BlockJacobi Preconditioner built
H1AMG: level = 7, num_edges = 553, nv = 100
BlockJacobi Preconditioner, constructor called, #blocks = 53
BlockJacobi Preconditioner built
H1AMG: level = 8, num_edges = 271, nv = 53
BlockJacobi Preconditioner, constructor called, #blocks = 28
BlockJacobi Preconditioner built
H1AMG: level = 9, num_edges = 126, nv = 28
BlockJacobi Preconditioner, constructor called, #blocks = 15
BlockJacobi Preconditioner built
H1AMG: level = 10, num_edges = 54, nv = 15
BlockJacobi Preconditioner, constructor called, #blocks = 8
BlockJacobi Preconditioner built
has inverse
assemble VOL element 54420/54420
WARNING: maxsteps is deprecated, use maxiter instead!
CG iteration 1, residual = 0.7094090868385201
CG iteration 2, residual = 0.277092354196473
CG iteration 3, residual = 0.2552141476493647
CG iteration 4, residual = 0.29760250572558
CG iteration 5, residual = 0.25515340506459033
CG iteration 6, residual = 0.19409338025273298
CG iteration 7, residual = 0.14466456735602215
CG iteration 8, residual = 0.11216525118555454
CG iteration 9, residual = 0.0795167297866193
CG iteration 10, residual = 0.05885836872647869
CG iteration 11, residual = 0.043432132001021806
CG iteration 12, residual = 0.03576010228039376
CG iteration 13, residual = 0.029804921900339124
CG iteration 14, residual = 0.021364235775509832
CG iteration 15, residual = 0.016395018482029945
CG iteration 16, residual = 0.013065067451515285
CG iteration 17, residual = 0.010281475047778715
CG iteration 18, residual = 0.0075161832386951115
CG iteration 19, residual = 0.005400599104160325
CG iteration 20, residual = 0.004159975246836071
CG iteration 21, residual = 0.0033356715080478648
CG iteration 22, residual = 0.0025567178563386563
CG iteration 23, residual = 0.0018863277812046933
CG iteration 24, residual = 0.0014480171690318302
CG iteration 25, residual = 0.0011583796766805852
CG iteration 26, residual = 0.0009066481187791878
CG iteration 27, residual = 0.0006879506314201771
CG iteration 28, residual = 0.0005269442608123841
CG iteration 29, residual = 0.0004011592733254342
CG iteration 30, residual = 0.0003150350082344221
CG iteration 31, residual = 0.0002498998602943328
CG iteration 32, residual = 0.00019082947428133485
CG iteration 33, residual = 0.0001431514175548389
CG iteration 34, residual = 0.0001117435655230187
CG iteration 35, residual = 8.567914626339054e-05
CG iteration 36, residual = 6.622157865058189e-05
CG iteration 37, residual = 5.077678888471302e-05
CG iteration 38, residual = 3.9347393964067174e-05
CG iteration 39, residual = 3.0699655930232356e-05
CG iteration 40, residual = 2.3329631346555676e-05
CG iteration 41, residual = 1.8101778951878397e-05
CG iteration 42, residual = 1.4422937256375272e-05
CG iteration 43, residual = 1.128070098701103e-05
CG iteration 44, residual = 8.67624883991305e-06
CG iteration 45, residual = 6.472767303048765e-06
CG iteration 46, residual = 5.003440601466715e-06
CG iteration 47, residual = 3.828388670957237e-06
CG iteration 48, residual = 2.928339674985158e-06
CG iteration 49, residual = 2.2656179101175973e-06
CG iteration 50, residual = 1.8273692600402287e-06
CG iteration 51, residual = 1.4226184082012495e-06
CG iteration 52, residual = 1.0818334558222385e-06
CG iteration 53, residual = 8.099502945603005e-07
CG iteration 54, residual = 6.09473074074458e-07
CG iteration 55, residual = 4.6194864798528714e-07
CG iteration 56, residual = 3.571209782788016e-07
CG iteration 57, residual = 2.7591527031657443e-07
CG iteration 58, residual = 2.182412897552229e-07
CG iteration 59, residual = 1.7485809206654988e-07
CG iteration 60, residual = 1.3431990604047457e-07
CG iteration 61, residual = 1.0077397347703597e-07
CG iteration 62, residual = 7.592589306656699e-08
CG iteration 63, residual = 5.952078091484223e-08
CG iteration 64, residual = 4.4861067028682956e-08
CG iteration 65, residual = 3.4204272871611885e-08
CG iteration 66, residual = 2.610924062797616e-08
CG iteration 67, residual = 1.9906599352018196e-08
CG iteration 68, residual = 1.5466948940629167e-08
CG iteration 69, residual = 1.1695566290271218e-08
CG iteration 70, residual = 8.963548384252506e-09
CG iteration 71, residual = 6.810820217702461e-09
CG iteration 72, residual = 5.212600493144689e-09
CG iteration 73, residual = 3.9848212512488375e-09
CG iteration 74, residual = 3.022515412432698e-09
CG iteration 75, residual = 2.299369048826489e-09
CG iteration 76, residual = 1.7707357293575882e-09
CG iteration 77, residual = 1.3495559669023768e-09
CG iteration 78, residual = 1.0254809347208245e-09
CG iteration 79, residual = 7.813152848881661e-10
CG iteration 80, residual = 6.02935469247742e-10
CG iteration 81, residual = 4.5959315327098883e-10
CG iteration 82, residual = 3.4386923428981863e-10
CG iteration 83, residual = 2.6574175505457817e-10
CG iteration 84, residual = 2.0321568056830468e-10
CG iteration 85, residual = 1.559833400122783e-10
CG iteration 86, residual = 1.2007149167737186e-10
CG iteration 87, residual = 9.753844388239724e-11
CG iteration 88, residual = 7.715165931082646e-11
CG iteration 89, residual = 5.86135120487688e-11
CG iteration 90, residual = 4.436208788493557e-11
CG iteration 91, residual = 3.399054505638281e-11
CG iteration 92, residual = 2.5650282759815758e-11
CG iteration 93, residual = 1.9751471755170407e-11
CG iteration 94, residual = 1.5010635692947355e-11
CG iteration 95, residual = 1.1254657180453063e-11
CG iteration 96, residual = 8.697086470015869e-12
CG iteration 97, residual = 6.646105916609159e-12
CG iteration 98, residual = 5.067918150282717e-12
CG iteration 99, residual = 3.791048771937065e-12
CG iteration 100, residual = 2.8942791634958148e-12
CG iteration 101, residual = 2.2093591918667863e-12
CG iteration 102, residual = 1.6751416406460215e-12
CG iteration 103, residual = 1.282319598981103e-12
CG iteration 104, residual = 9.832638543054068e-13
CG iteration 105, residual = 7.67093444418681e-13
CG iteration 106, residual = 6.068687645511326e-13

[9]:

BaseWebGuiScene

Postscript¶

By popular demand, here is the code to draw the figure found at the beginning of this tutorial:

[10]:

from netgen.geom2d import unit_square
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
fes_ho = Discontinuous(H1(mesh, order=10))
fes_lo = H1(mesh, order=1, dirichlet=".*")
fes_lam = Discontinuous(H1(mesh, order=1))
fes = FESpace([fes_ho, fes_lo, fes_lam])
uho, ulo, lam = fes.TrialFunction()

a = BilinearForm(fes)
a += Variation(0.5 * grad(uho)*grad(uho)*dx
               - 1*uho*dx
               + (uho-ulo)*lam*dx(element_vb=BBND))
gfu = GridFunction(fes)
solvers.Newton(a=a, u=gfu)
Draw(gfu.components[0],deformation=True)

 Generate Mesh from spline geometry
 Boundary mesh done, np = 40
 CalcLocalH: 40 Points 0 Elements 0 Surface Elements
 Meshing domain 1 / 1
 Surface meshing done
 Edgeswapping, topological
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Update mesh topology
Newton iteration  0
 Update clusters
Assemble linearization
assemble VOL element 232/232
call umfpack ... done
err =  0.39392955469293095
Newton iteration  1
Assemble linearization
assemble VOL element 232/232
call umfpack ... done
err =  1.7898870223932246e-15

[10]:

BaseWebGuiScene

[ ]: