This page was generated from wta/adaptivity.ipynb.

Adaptivity

from ngsolve import *
from netgen.occ import *
from ngsolve.webgui import Draw

Define the geometry by 2D Netgen-OpenCascade modeling: Define rectangles and polygones, and glue them together to one shape object. OCC maintains the full geometry topology of vertices, edges, faces and solids.

def MakeGeometry():
    base = Rectangle(1, 0.6).Face()
    chip = MoveTo(0.5,0.15).Line(0.15,0.15).Line(-0.15,0.15).Line(-0.15,-0.15).Close().Face()
    top = MoveTo(0.2,0.6).Rectangle(0.6,0.2).Face()
    base -= chip

    base.faces.name="base"
    chip.faces.name="chip"
    chip.faces.col=(1,0,0)
    top.faces.name="top"
    geo = Glue([base,chip,top])
    geo.edges.name="default"
    geo.edges.Min(Y).name="bot"
    Draw(geo)
    return geo

geo = MakeGeometry()

Piece-wise constant coefficients in sub-domains:

mesh = geo.GenerateMesh(maxh=0.2, dim=2)
print (mesh.GetMaterials())

('base', 'chip', 'top')

fes = H1(mesh, order=3, dirichlet="bot", autoupdate=True)
u, v = fes.TnT()

lam = mesh.MaterialCF( { "base" : 1, "chip" : 1000, "top" : 20 } )
a = BilinearForm(lam*grad(u)*grad(v)*dx)

# heat-source in inner subdomain
f = LinearForm(1*v*dx(definedon="chip"))

c = preconditioners.MultiGrid(a, inverse="sparsecholesky")

gfu = GridFunction(fes)

Assemble and solve problem:

def SolveBVP():
    a.Assemble()
    f.Assemble()
    inv = CGSolver(a.mat, c.mat)
    gfu.vec.data = inv * f.vec

SolveBVP()
Draw (gfu, mesh);

Gradient recovery error estimator: Interpolate finite element flux

\[q_h := I_h (\lambda \nabla u_h)\]

and take difference as element error indicator:

\[\eta_T := \tfrac{1}{\lambda} \| q_h - \lambda \nabla u_h \|_{L_2(T)}^2\]

l = []    # l = list of estimated total error
space_flux = HDiv(mesh, order=2, autoupdate=True)
gf_flux = GridFunction(space_flux, "flux", autoupdate=True)

def CalcError():

    flux = lam * grad(gfu)   # the FEM-flux
    gf_flux.Set(flux)        # interpolate into H(div)

    # compute estimator:
    err = 1/lam*(flux-gf_flux)*(flux-gf_flux)
    eta2 = Integrate(err, mesh, VOL, element_wise=True)
    l.append ((fes.ndof, sqrt(sum(eta2))))
    print("ndof =", fes.ndof, " toterr =", sqrt(sum(eta2)))

    # mark for refinement:
    maxerr = max(eta2)
    # marking with Python loop:
    # for el in mesh.Elements():
    #    mesh.SetRefinementFlag(el, eta2[el.nr] > 0.25*maxerr)

    # marking using numpy vectorization:
    mesh.ngmesh.Elements2D().NumPy()["refine"] = eta2.NumPy() > 0.25*maxerr

CalcError()

ndof = 208  toterr = 0.006210901700080951

Adaptive loop:

level = 0
while fes.ndof < 50000:
    mesh.Refine()
    SolveBVP()
    CalcError()
    level = level+1
    if level%5 == 0:
        Draw (gfu)

ndof = 328  toterr = 0.00543432380249667
ndof = 583  toterr = 0.0034474161171856982
ndof = 997  toterr = 0.002477627265012361
ndof = 1492  toterr = 0.0017641880137191854
ndof = 2158  toterr = 0.0011758942564355941

ndof = 2950  toterr = 0.0007720685013193737
ndof = 3826  toterr = 0.0005050543888604478
ndof = 4651  toterr = 0.00033457393100878386
ndof = 5422  toterr = 0.000226275216509452
ndof = 6121  toterr = 0.00015855832952391946

ndof = 6586  toterr = 0.000127871788509995
ndof = 7321  toterr = 9.644005521450921e-05
ndof = 8200  toterr = 7.791024979152021e-05
ndof = 9184  toterr = 6.0827084437190935e-05
ndof = 9895  toterr = 5.020406998256112e-05

ndof = 11209  toterr = 3.9135252075147564e-05
ndof = 12994  toterr = 2.805369239510877e-05
ndof = 14365  toterr = 2.327351170086093e-05
ndof = 16252  toterr = 1.848631827808821e-05
ndof = 18613  toterr = 1.4268464429385618e-05

ndof = 21763  toterr = 1.0776539402828711e-05
ndof = 25099  toterr = 8.414670493657838e-06
ndof = 28927  toterr = 6.561005754203283e-06
ndof = 33445  toterr = 5.037685791968596e-06
ndof = 38899  toterr = 3.844396993288887e-06

ndof = 45985  toterr = 2.901169912002367e-06
ndof = 53179  toterr = 2.277812847839709e-06

Draw (gfu);

%matplotlib inline
import matplotlib.pyplot as plt
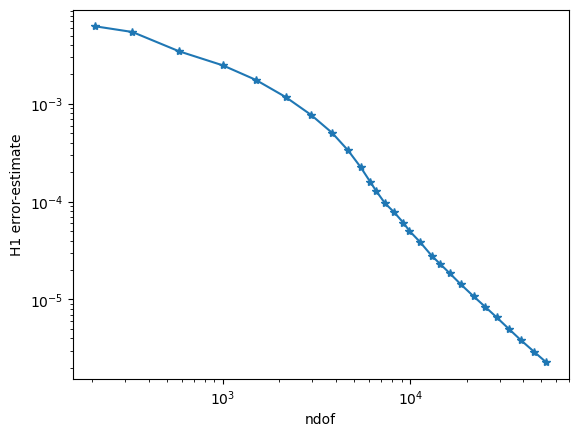
plt.yscale('log')
plt.xscale('log')
plt.xlabel("ndof")
plt.ylabel("H1 error-estimate")
ndof,err = zip(*l)
plt.plot(ndof,err, "-*")

plt.ion()
plt.show();