Symbolic definition of forms : magnetic field¶
We compute the magnetic field generated by a coil placed on a C-core. We see how to
model a 3D constructive solid geometry
set material properties from domain and boundary labels
define bilinear- and linear forms symbolically using trial- and testfunctions
Download cmagnet.py
from netgen.occ import *
from ngsolve import *
def MakeGeometry():
box = Box((-1,-1,-1), (2,1,2))
box.faces.name = "outer"
core = Box((0,-0.05,0), (0.8,0.05,1)) - \
Box((0.1,-1,0.1), (0.7,1,0.9)) - \
Box((0.5,-1,0.4), (1,1,0.6))
core.solids.name = "core"
core.solids.maxh = 0.03
coil = Cylinder((0.05,0,0.3), (0,0,1), 0.3, 0.4) - \
Cylinder((0.05,0,0.3), (0,0,1), 0.15, 0.4)
coil.solids.name = "coil"
air = box - core - coil
air.solids.name = "air"
return Glue([core, coil, air])
mesh = MakeGeometry().GenerateMesh(maxh=0.5)
# curve elements for geometry approximation
mesh.Curve(5)
ngsglobals.msg_level = 5
fes = HCurl(mesh, order=4, dirichlet="outer", nograds = True)
# u and v refer to trial and test-functions in the definition of forms below
u = fes.TrialFunction()
v = fes.TestFunction()
mur = mesh.MaterialCF({ "core" : 1000 }, default=1)
mu0 = 1.257e-6
nu = 1/(mu0*mur)
a = BilinearForm(fes, symmetric=True)
a += nu*curl(u)*curl(v)*dx + 1e-6*nu*u*v*dx
c = Preconditioner(a, type="bddc")
# c = Preconditioner(a, type="multigrid", flags = { "smoother" : "block" } )
f = LinearForm(fes)
f += CoefficientFunction((y,0.05-x,0)) * v * dx("coil")
u = GridFunction(fes)
with TaskManager():
a.Assemble()
f.Assemble()
solver = CGSolver(mat=a.mat, pre=c.mat)
u.vec.data = solver * f.vec
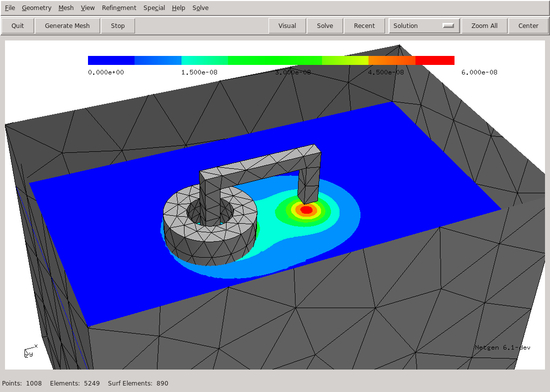
Draw (u.Deriv(), mesh, "B-field", draw_surf=False)
Mesh and magnitude of magnetic field visualized in Netgen: