This page was generated from unit-9.3-highorder/highorder.ipynb.
9.3 High Order Finite Elements¶
Finite elements implement the basis functions: myHOElement.hpp myHOElement.cpp
Finite element spaces implement the enumeration of degrees of freedom, and creation of elements: myHOFESpace.hpp myHOFESpace.cpp
[1]:
from ngsolve.fem import CompilePythonModule
from pathlib import Path
m = CompilePythonModule(Path('mymodule.cpp'), init_function_name='mymodule')
called mymodule
[2]:
from netgen.occ import unit_square
from ngsolve import *
from ngsolve.webgui import Draw
mesh = Mesh(unit_square.GenerateMesh(maxh=0.2, quad_dominated=False))
We can now create an instance of our own finite element space:
[3]:
fes = m.MyHighOrderFESpace(mesh, order=4, dirichlet="left|bottom|top")
and use it within NGSolve such as the builtin finite element spaces:
[4]:
print ("ndof = ", fes.ndof)
ndof = 473
[5]:
gfu = GridFunction(fes)
gfu.Set(x*x*y*y)
Draw (gfu)
Draw (grad(gfu)[0], mesh);
and solve the standard problem:
[6]:
u,v = fes.TnT()
a = BilinearForm(grad(u)*grad(v)*dx).Assemble()
f = LinearForm(10*v*dx).Assemble()
gfu.vec.data = a.mat.Inverse(fes.FreeDofs())*f.vec
Draw (gfu, order=3);
[7]:
errlist = []
for p in range(1,13):
fes = m.MyHighOrderFESpace(mesh, order=p)
func = sin(pi*x)*sin(pi*y)
gfu = GridFunction(fes)
gfu.Set(func)
err = sqrt(Integrate( (func-gfu)**2, mesh, order=5+2*p))
errlist.append((p,err))
print (errlist)
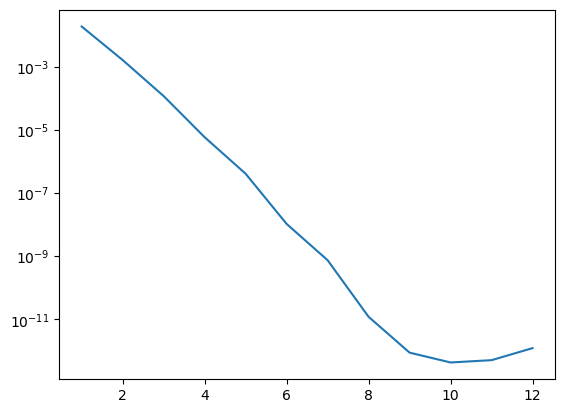
[(1, 0.020177922673693338), (2, 0.0015949321640548715), (3, 0.00013347307605740216), (4, 5.7001970136187035e-06), (5, 4.842564786630887e-07), (6, 1.0227227430075864e-08), (7, 9.060913101724547e-10), (8, 1.169168476838992e-11), (9, 1.0865918104164566e-12), (10, 3.9432643865379776e-13), (11, 6.918885483553872e-13), (12, 1.2959645263307293e-12)]
[8]:
import matplotlib.pyplot as plt
n,err = zip(*errlist)
plt.yscale('log')
plt.plot(n,err);
Exercises:
Extend MyHighOrderFESpace by high order quadrilateral elements.
http://www.numa.uni-linz.ac.at/Teaching/PhD/Finished/zaglmayr-diss.pdf, page 68 ff
[ ]: