This page was generated from unit-3.5-surfacehdg/surfacehdg.ipynb.

3.5 Scalar PDE on surfaces (with HDG)

We are solving the scalar linear transport problem

\[\partial_t u - \varepsilon \Delta_\Gamma u + \operatorname{div}_\Gamma ( \mathbf{w} u ) = 0 \quad \text{ on } \Gamma,\]

where \(\Gamma\) is a closed oriented surface in \(\mathbb{R}^3\).

from ngsolve import *
import netgen.gui
from math import pi

Mesh of (only) the surface:

We consider the unit sphere (only surface mesh!)

from netgen.csg import *
geo = CSGeometry()
geo.Add(Sphere(Pnt(0,0,0),1).bc("sphere"))

0

from netgen.meshing import MeshingParameters
from netgen.meshing import MeshingStep
mp = MeshingParameters(maxh=0.5, perfstepsend = MeshingStep.MESHSURFACE)

mesh = Mesh(geo.GenerateMesh(mp=mp))

 Start Findpoints
 main-solids: 1
 Found points 0
 Analyze spec points
 Find edges
 0 edges found
 Check intersecting edges
 CalcLocalH: 2 Points 0 Elements 0 Surface Elements
 Start Findpoints
 main-solids: 1
 Found points 0
 Analyze spec points
 Find edges
 0 edges found
 Check intersecting edges
 Start Findpoints
 main-solids: 1
 Found points 0
 Analyze spec points
 Find edges
 0 edges found
 Check intersecting edges
 Surface 1 / 1
 load internal triangle rules
 Surface meshing done
 0 illegal triangles
 Optimize Surface
 Edgeswapping, topological
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Combine improve
 Smoothing
 126 elements, 65 points
 SplitSeparateFaces
 Update mesh topology
 Update clusters

order = 4
if order > 0:
    mesh.Curve(order)
Draw(mesh)

 Curve elements, order = 4
 Update clusters
 Curving edges
 Curving faces

Tangential velocity field:

t = Parameter(0.)
b = CoefficientFunction((y,-x,0))
Draw (b, mesh, "b")
eps = 5e-5

some local quantities

normal, tangential, co-normal and mesh size

n = specialcf.normal(mesh.dim)
h = specialcf.mesh_size
local_tang = specialcf.tangential(mesh.dim)
con = Cross(n,local_tang) #co-normal pointing outside of a surface element
bn = InnerProduct(b,con)

Discretization

Surface FESpaces:

fesl2 = SurfaceL2(mesh, order=order)
fesedge = FacetSurface(mesh, order=order)

fes = FESpace([fesl2,fesedge])
u,uE = fes.TrialFunction()
v,vE = fes.TestFunction()

surface gradients, co-normal derivatives and jumps:

gradu = u.Trace().Deriv()
gradv = v.Trace().Deriv()
jumpu = u - uE
jumpv = v - vE
dudn = InnerProduct(gradu,con)
dvdn = InnerProduct(gradv,con)

Diffusion formulation (Hybrid Interior Penalty on Surface):

\[ \sum_T \int_T \nabla u \nabla v - \sum_T \int_{\partial T} n \nabla u (v-\widehat v) - \sum_T \int_{\partial T} n \nabla u (u-\widehat u) + \frac{\alpha p^2}{h} \sum_F \int_F (u-\widehat u)(v-\widehat v)\]

a = BilinearForm(fes)
# diffusion

dr = ds(element_boundary=True)

alpha = 10*(order+1)**2
a += eps*gradu * gradv * ds
a += - eps*dudn * jumpv * dr
a += - eps*dvdn * jumpu * dr
a += eps*alpha/h * jumpu * jumpv * dr

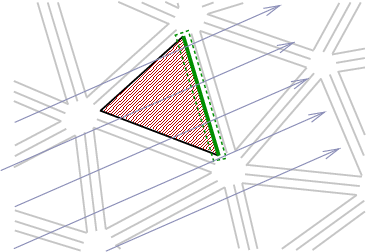
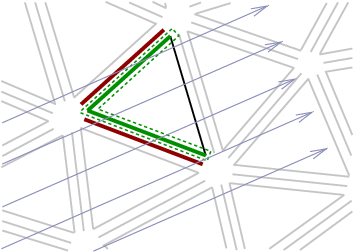
Convection formulation (Hybrid Upwinding):

\[ \sum_T \int_T - u \mathbf{w} \cdot \nabla v + \sum_T \int_{\partial T} (\mathbf{w} \cdot \mathbf{n}) u^{hyb-upw} v + \sum_T \int_{\partial T_{out}} (\mathbf{w} \cdot \mathbf{n}) (\hat{u} - u) \hat{v}\]

with

\[\begin{split}u^{hyb-upw} = \left\{ \begin{array}{cll} u & \text{if } \mathbf{w} \cdot \mathbf{n} & (outflow), \\ \hat{u} & \text{else} & (inflow) . \end{array} \right.\end{split}\]

outflow	inflow

a = BilinearForm(fes)
# convection (surface version of Egger+Schöberl formulation):
a += - u * InnerProduct(b,gradv) * ds
a += IfPos(bn, bn*u, bn*uE) * v * dr + IfPos(bn, bn, 0) * (uE - u) * vE * dr
a.Assemble()

assemble BND element 124/124

<ngsolve.comp.BilinearForm at 0x7f4524dd9c30>

Mass matrix:

m = BilinearForm(fes)
m += u*v*ds
m.Assemble()

assemble BND element 124/124

<ngsolve.comp.BilinearForm at 0x7f4524e03230>

\(M^\ast\)-matrix for implicit Euler

dt = 0.02

mstar = m.mat.CreateMatrix()
mstar.AsVector().data = m.mat.AsVector() + dt * a.mat.AsVector()
mstarinv = mstar.Inverse()

from math import pi
T = 8*pi

call pardiso ... done

Time stepping

Visualization of solution (Deformation in normal direction)

gfu = GridFunction(fes)
gfu.components[0].Set(1.5*exp(-20*(x*x+(y-1)**2+(z)**2)),definedon=mesh.Boundaries("sphere"))
Draw (gfu.components[0], mesh, "u")
Draw (gfu.components[0]*n, mesh, "un", sd=4, autoscale=False)
res = gfu.vec.CreateVector()
SetVisualization(deformation=True)

setvalues element 124/124

The time loop

t.Set(0)
for i in range(int(T/dt)):
    res.data = m.mat * gfu.vec
    gfu.vec.data = mstarinv * res
    Redraw(blocking=True)
    t.Set(t.Get()+dt)

Remark:

• We can apply static condensation as in the volume