This page was generated from unit-2.10-dualbasis/dualbasis.ipynb.

2.10 Dual basis functions¶

We use dual basis functions to define interpolation operators, define transfer operators between different finite element spaces, and auxiliar space preconditioners.

Canonical interpolation¶

The canonical finite element interpolation operator is defined by specifying the degrees of freedom. For low order methods these are typically nodal values, while for high order methods these are most often moments. For example, the interpolation of a function \(u\) onto the \(p^{th}\) order triangle is given by: find \(u_{hp} \in V_{hp}\) such that

\begin{eqnarray*} u_{hp} (V) & = & u(V) \quad \forall \text{ vertices } V \\ \int_E u_{hp} q & = & \int_E u q \quad \forall q \in P^{p-2}(E) \; \forall \text{ edges } E \\ \int_T u_{hp} q & = & \int_T u q \quad \forall q \in P^{p-3}(T) \; \forall \text{ triangles } T \end{eqnarray*}

[1]:

import netgen.gui
from ngsolve import *
from netgen.geom2d import unit_square
import matplotlib.pylab as plt
mesh = Mesh(unit_square.GenerateMesh(maxh=2))

The NGSolve ‘Set’ function does local projection, and simple averaging. In particular, this does not respect point values in mesh vertices.

[2]:

fes = H1(mesh, order=3, low_order_space=False)

func = x*x*x*x
gfu = GridFunction(fes)
gfu.Set(func)
Draw (gfu)
print (gfu.vec)

 -0.0223792
 0.991843
 0.977621
 -0.00815655
 3.34984
 2.19912
 3.34984
       2
 0.00660131
 -6.05333e-15
 0.00660131
 -1.15463e-14
 3.34984
 -1.80088
 -2.17601
 1.82399

Most NGSolve finite element spaces provide now a “dual” operator, which delivers the moments (i.e. the dual space basis functions) instead of function values. The integrals over faces, edges and also vertices are defined by co-dimension 1 (=BND), co-dimension 2 (=BBND) or co-dimension 3 (=BBBND) integrals over the volume elements. We define a variational problem for canonical interpolaion:

[3]:

u,v = fes.TnT()
vdual = v.Operator("dual")

a = BilinearForm(fes)
a += u*vdual*dx + u*vdual*dx(element_vb=BND) + \
    u*vdual*dx(element_vb=BBND)
a.Assemble()

f = LinearForm(fes)
f += func*vdual*dx + func*vdual*dx(element_vb=BND) + \
    func*vdual*dx(element_vb=BBND)
f.Assemble()

# interpolation in vertices preserves values 0 and 1
gfu.vec.data = a.mat.Inverse() * f.vec
print (gfu.vec)
Draw (gfu)

       0
       1
       1
       0
     3.6
       2
     3.6
       2
       0
       0
 -8.66668e-32
 -1.66533e-15
     3.6
      -2
      -2
       2

The vertex degrees of freedom vanish for edge and element basis functions, and the edge degrees of freedom vanish for element basis functions, but not vise versa. Thus, the obtained matrix A is block-triangular:

[4]:

import scipy.sparse as sp
A = sp.csr_matrix(a.mat.CSR())
plt.rcParams['figure.figsize'] = (4,4)
plt.spy(A)
plt.show()

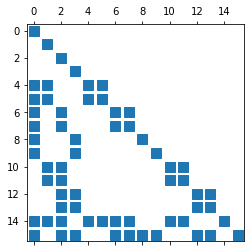
../../_images/i-tutorials_unit-2.10-dualbasis_dualbasis_8_0.png

We can use proper block Gauss-Seidel smoothing for solving with that block triangular matrix by blocking the dofs for the individual vertices, edges and elements. Since the NGSolve Gauss-Seidel smoother reorders the order of smoothing blocks for parallelization, we have to take care to first compute vertex values, then edge values, and finally element values by running three different Gauss-Seidel sweeps.

[5]:

vblocks = [fes.GetDofNrs(vertex) for vertex in mesh.vertices]
eblocks = [fes.GetDofNrs(edge) for edge in mesh.edges]
fblocks = [fes.GetDofNrs(face) for face in mesh.faces]

print (vblocks)
print (eblocks)
print (fblocks)

vinv = a.mat.CreateBlockSmoother(vblocks)
einv = a.mat.CreateBlockSmoother(eblocks)
finv = a.mat.CreateBlockSmoother(fblocks)

vinv.Smooth(gfu.vec, f.vec)
einv.Smooth(gfu.vec, f.vec)
finv.Smooth(gfu.vec, f.vec)
print (gfu.vec)

[(0,), (1,), (2,), (3,)]
[(4, 5), (6, 7), (8, 9), (10, 11), (12, 13)]
[(14,), (15,)]
       0
       1
       1
       0
     3.6
       2
     3.6
       2
       0
       0
 -8.66668e-32
 -1.66533e-15
     3.6
      -2
      -2
       2

Embedding Finite Element Spaces¶

This interpolation can be used to transform functions from one finite element space \(V_{src}\) to another one \(V_{dst}\). We use the dual space of the destination space:

\[\int_{node} u_{dst} v_{dual} = \int_{node} u_{src} v_{dual} \qquad \forall \, v_{dual} \; \forall \, \text{nodes}\]

The left hand side leads to a non-symmetric square matrix, the right hand side to a rectangular matrix.

As an example we implement the transformation from an vector valued \(H^1\) space into \(H(\operatorname{div})\):

[6]:

import netgen.gui
from ngsolve import *
from netgen.geom2d import unit_square

mesh = Mesh(unit_square.GenerateMesh(maxh=0.2))

fesh1 = VectorH1(mesh, order=2)
feshdiv = HDiv(mesh, order=2)

gfuh1 = GridFunction(fesh1)
gfuh1.Set ( (x*x,y*y) )

gfuhdiv = GridFunction(feshdiv, name="uhdiv")

Build the matrices, and use a direct solver:

[7]:

amixed = BilinearForm(trialspace=fesh1, testspace=feshdiv)
ahdiv = BilinearForm(feshdiv)

u,v = feshdiv.TnT()
vdual = v.Operator("dual")
uh1 = fesh1.TrialFunction()

dS = dx(element_boundary=True)
ahdiv += u*vdual * dx + u*vdual * dS
ahdiv.Assemble()

amixed += uh1*vdual*dx + uh1*vdual*dS
amixed.Assemble()

# build transformation operator:
transform = ahdiv.mat.Inverse() @ amixed.mat
gfuhdiv.vec.data = transform * gfuh1.vec

Draw (gfuh1)
Draw (gfuhdiv)

We implement a linear operator performing the fast conversion by Gauss-Seidel smoothing:

[8]:

class MyBlockInverse(BaseMatrix):
    def __init__ (self, mat, eblocks, fblocks):
        super(MyBlockInverse, self).__init__()
        self.mat = mat
        self.einv = mat.CreateBlockSmoother(eblocks)
        self.finv = mat.CreateBlockSmoother(fblocks)
        self.res = self.mat.CreateColVector()

    def CreateRowVector(self):
        return self.mat.CreateColVector()
    def CreateColVector(self):
        return self.mat.CreateRowVector()

    def Mult(self, x, y):
        # y[:] = 0
        # self.einv.Smooth(y,x)    #   y = y +  A_E^-1  (x - A y)
        # self.finv.Smooth(y,x)    #   y = y +  A_E^-1  (x - A y)

        # the same, but we see how to transpose that
        y.data = self.einv * x
        self.res.data = x - self.mat * y
        y.data += finv * self.res

    def MultTrans(self, x, y):
        y.data = self.finv.T * x
        self.res.data = x - self.mat.T * y
        y.data += einv.T * self.res


eblocks = [feshdiv.GetDofNrs(edge) for edge in mesh.edges]
fblocks = [feshdiv.GetDofNrs(face) for face in mesh.faces]

transform = MyBlockInverse(ahdiv.mat, eblocks, fblocks) @ amixed.mat
gfuhdiv.vec.data = transform * gfuh1.vec

Auxiliary Space Preconditioning¶

Nepomnyaschikh 91, Hiptmair-Xu 07, ….

Assume we have a complicated problem with some complicated discretization, and we have good preconditioners for a nodal finite element discretization for the Laplace operator. By auxiliary space preconditioning we can reuse the simple preconditioners for the complicated problems. It is simple, and works well in many cases.

As a simple example, we precondition a DG discretization by an \(H^1\) conforming method.

[9]:

mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))

The DG discretization:

[10]:

order=4
fesDG = L2(mesh, order=order, dgjumps=True)
u,v = fesDG.TnT()
aDG = BilinearForm(fesDG)
jump_u = u-u.Other()
jump_v = v-v.Other()
n = specialcf.normal(2)
mean_dudn = 0.5*n * (grad(u)+grad(u.Other()))
mean_dvdn = 0.5*n * (grad(v)+grad(v.Other()))
alpha = 4
h = specialcf.mesh_size
aDG = BilinearForm(fesDG)
aDG += grad(u)*grad(v) * dx
aDG += alpha*order**2/h*jump_u*jump_v * dx(skeleton=True)
aDG += alpha*order**2/h*u*v * ds(skeleton=True)
aDG += (-mean_dudn*jump_v -mean_dvdn*jump_u) * dx(skeleton=True)
aDG += (-n*grad(u)*v-n*grad(v)*u)* ds(skeleton=True)
aDG.Assemble()

fDG = LinearForm(fesDG)
fDG += 1*v * dx
fDG.Assemble()
gfuDG = GridFunction(fesDG)

The auxiliary \(H^1\) discretization:

[11]:

fesH1 = H1(mesh, order=2, dirichlet=".*")
u,v = fesH1.TnT()
aH1 = BilinearForm(fesH1)
aH1 += grad(u)*grad(v)*dx
preH1 = Preconditioner(aH1, "bddc")
aH1.Assemble()

[12]:

transform = fesH1.ConvertL2Operator(fesDG)
pre = transform @ preH1.mat @ transform.T + aDG.mat.CreateSmoother()

solvers.CG(mat=aDG.mat, rhs=fDG.vec, sol=gfuDG.vec, pre=pre, \
           maxsteps=200)

Draw (gfuDG)

it =  0  err =  0.25284243668046297
it =  1  err =  0.032978067384425123
it =  2  err =  0.008565533056584773
it =  3  err =  0.003350791073888934
it =  4  err =  0.0012352250386188544
it =  5  err =  0.0008953027379470017
it =  6  err =  0.0009408102631568254
it =  7  err =  0.001042854167877386
it =  8  err =  0.0008241218795830281
it =  9  err =  0.0006517325370371805
it =  10  err =  0.0005341681600736627
it =  11  err =  0.0004077364183233898
it =  12  err =  0.0003505773304178867
it =  13  err =  0.0003315354815667259
it =  14  err =  0.0002880358057303521
it =  15  err =  0.00023121545894290218
it =  16  err =  0.00018655018570322158
it =  17  err =  0.0001315769501463096
it =  18  err =  9.23017402208531e-05
it =  19  err =  7.485395694725874e-05
it =  20  err =  7.2070463553889e-05
it =  21  err =  5.9713438908780945e-05
it =  22  err =  4.98296950901793e-05
it =  23  err =  4.120697126466611e-05
it =  24  err =  3.4176489903350796e-05
it =  25  err =  2.976504717416849e-05
it =  26  err =  3.0227068897512407e-05
it =  27  err =  2.9571437689575053e-05
it =  28  err =  2.569037314973355e-05
it =  29  err =  2.020293864722458e-05
it =  30  err =  1.7555484171467588e-05
it =  31  err =  1.3996042684633619e-05
it =  32  err =  1.156752412736829e-05
it =  33  err =  1.0573917718225916e-05
it =  34  err =  9.869130802508034e-06
it =  35  err =  7.96820282829413e-06
it =  36  err =  6.50276185527305e-06
it =  37  err =  4.73456524452765e-06
it =  38  err =  4.169406582626635e-06
it =  39  err =  3.740963548259307e-06
it =  40  err =  3.514880805177166e-06
it =  41  err =  3.0503864090218075e-06
it =  42  err =  2.7094137652640254e-06
it =  43  err =  2.0765520405670668e-06
it =  44  err =  1.6480108115367602e-06
it =  45  err =  1.4746781727859935e-06
it =  46  err =  1.4114503319110791e-06
it =  47  err =  1.4006035122626704e-06
it =  48  err =  1.1481091661337843e-06
it =  49  err =  9.279751292278777e-07
it =  50  err =  7.684324049141674e-07
it =  51  err =  6.343737423516011e-07
it =  52  err =  5.868300135073913e-07
it =  53  err =  5.483251077316992e-07
it =  54  err =  4.601522921980077e-07
it =  55  err =  3.565427242527408e-07
it =  56  err =  2.7937302419448216e-07
it =  57  err =  2.4660330710811e-07
it =  58  err =  2.0116576888678727e-07
it =  59  err =  1.744152825885444e-07
it =  60  err =  1.552070033063774e-07
it =  61  err =  1.2841858136452377e-07
it =  62  err =  9.985763939316339e-08
it =  63  err =  8.088567260257493e-08
it =  64  err =  6.48219742479612e-08
it =  65  err =  5.7882787754852235e-08
it =  66  err =  5.155782466351511e-08
it =  67  err =  4.207825530042199e-08
it =  68  err =  3.3494446098751474e-08
it =  69  err =  2.6848671146329606e-08
it =  70  err =  2.1423564036207714e-08
it =  71  err =  1.8330570047070252e-08
it =  72  err =  1.735335427381623e-08
it =  73  err =  1.518534436998033e-08
it =  74  err =  1.3273851059295169e-08
it =  75  err =  1.0106789943533495e-08
it =  76  err =  7.98773506338513e-09
it =  77  err =  6.969750611402814e-09
it =  78  err =  6.5144315988731806e-09
it =  79  err =  6.059090244107737e-09
it =  80  err =  4.875319110152476e-09
it =  81  err =  3.861739632256915e-09
it =  82  err =  2.9665506557761113e-09
it =  83  err =  2.399560833927694e-09
it =  84  err =  2.181292606974908e-09
it =  85  err =  2.036305946180916e-09
it =  86  err =  1.6651955248891882e-09
it =  87  err =  1.2832584725938827e-09
it =  88  err =  9.670470717099418e-10
it =  89  err =  7.828922295056368e-10
it =  90  err =  6.674761619789713e-10
it =  91  err =  6.034124108270938e-10
it =  92  err =  5.644283824459128e-10
it =  93  err =  4.4825504225065944e-10
it =  94  err =  3.444048804836416e-10
it =  95  err =  2.822345403365758e-10
it =  96  err =  2.488526040480442e-10
it =  97  err =  2.3077537561975838e-10
it =  98  err =  2.1687408144691415e-10
it =  99  err =  1.8635701609514505e-10
it =  100  err =  1.478970128699429e-10
it =  101  err =  1.2184697586515409e-10
it =  102  err =  1.032272623535994e-10
it =  103  err =  9.423570811706813e-11
it =  104  err =  8.63000025459307e-11
it =  105  err =  7.2410470224483e-11
it =  106  err =  6.044463785983903e-11
it =  107  err =  4.8845599848640266e-11
it =  108  err =  3.8961010080373866e-11
it =  109  err =  3.5352574587577117e-11
it =  110  err =  3.240033926746499e-11
it =  111  err =  2.9325926418511466e-11
it =  112  err =  2.386108295503846e-11
it =  113  err =  1.8036111373241942e-11
it =  114  err =  1.4201873909250685e-11
it =  115  err =  1.248787943533406e-11
it =  116  err =  1.194634240968124e-11
it =  117  err =  1.1170089326431057e-11
it =  118  err =  9.282104090324566e-12
it =  119  err =  7.2696469189283465e-12
it =  120  err =  5.437900470884417e-12
it =  121  err =  4.592761208204951e-12
it =  122  err =  4.2468889918769625e-12
it =  123  err =  3.775664705110664e-12
it =  124  err =  3.151316347234727e-12
it =  125  err =  2.481047631811683e-12
it =  126  err =  1.9419938690551673e-12
it =  127  err =  1.562020436661743e-12
it =  128  err =  1.4068736654605672e-12
it =  129  err =  1.2884101157515056e-12
it =  130  err =  1.0984594195197223e-12
it =  131  err =  8.723376773216862e-13
it =  132  err =  6.502467151576821e-13
it =  133  err =  5.412731820121117e-13
it =  134  err =  4.83075736590747e-13
it =  135  err =  4.3125111374855284e-13
it =  136  err =  3.811516206776204e-13
it =  137  err =  3.195338478382081e-13
it =  138  err =  2.378972973439802e-13

[ ]: