This page was generated from unit-2.1.3-bddc/bddc.ipynb.
2.1.3 Element-wise BDDC Preconditioner¶
The element-wise BDDC (Balancing Domain Decomposition preconditioner with Constraints) preconditioner in NGSolve is a good general purpose preconditioner that works well both in the shared memory parallel mode as well as in distributed memory mode. In this tutorial, we discuss this preconditioner, related built-in options, and customization from python.
Let us start with a simple description of the element-wise BDDC in the context of Lagrange finite element space \(V\). Here the BDDC preconditoner is constructed on an auxiliary space \(\widetilde{V}\) obtained by connecting only element vertices (leaving edge and face shape functions discontinuous). Although larger, the auxiliary space allows local elimination of edge and face variables. Hence an analogue of the original matrix \(A\) on this space, named \(\widetilde A\), is less expensive to invert. This inverse is used to construct a preconditioner for \(A\) as follows:
Here, \(R\) is the averaging operator for the discontinous edge and face variables.
To construct a general purpose BDDC preconditioner, NGSolve generalizes this idea to all its finite element spaces by a classification of degrees of freedom. Dofs are classified into (condensable) LOCAL_DOFs that we saw in 1.4 and a remainder that includes these types:
WIREBASKET_DOFINTERFACE_DOFThe original finite element space \(V\) is obtained by requiring conformity of both the above types of dofs, while the auxiliary space \(\widetilde{V}\) is obtained by requiring conformity of WIREBASKET_DOFs only.
Here is a figure of a typical function in the default \(\widetilde{V}\) (and the code to generate this is at the end of this tutorial) when \(V\) is the Lagrange space:
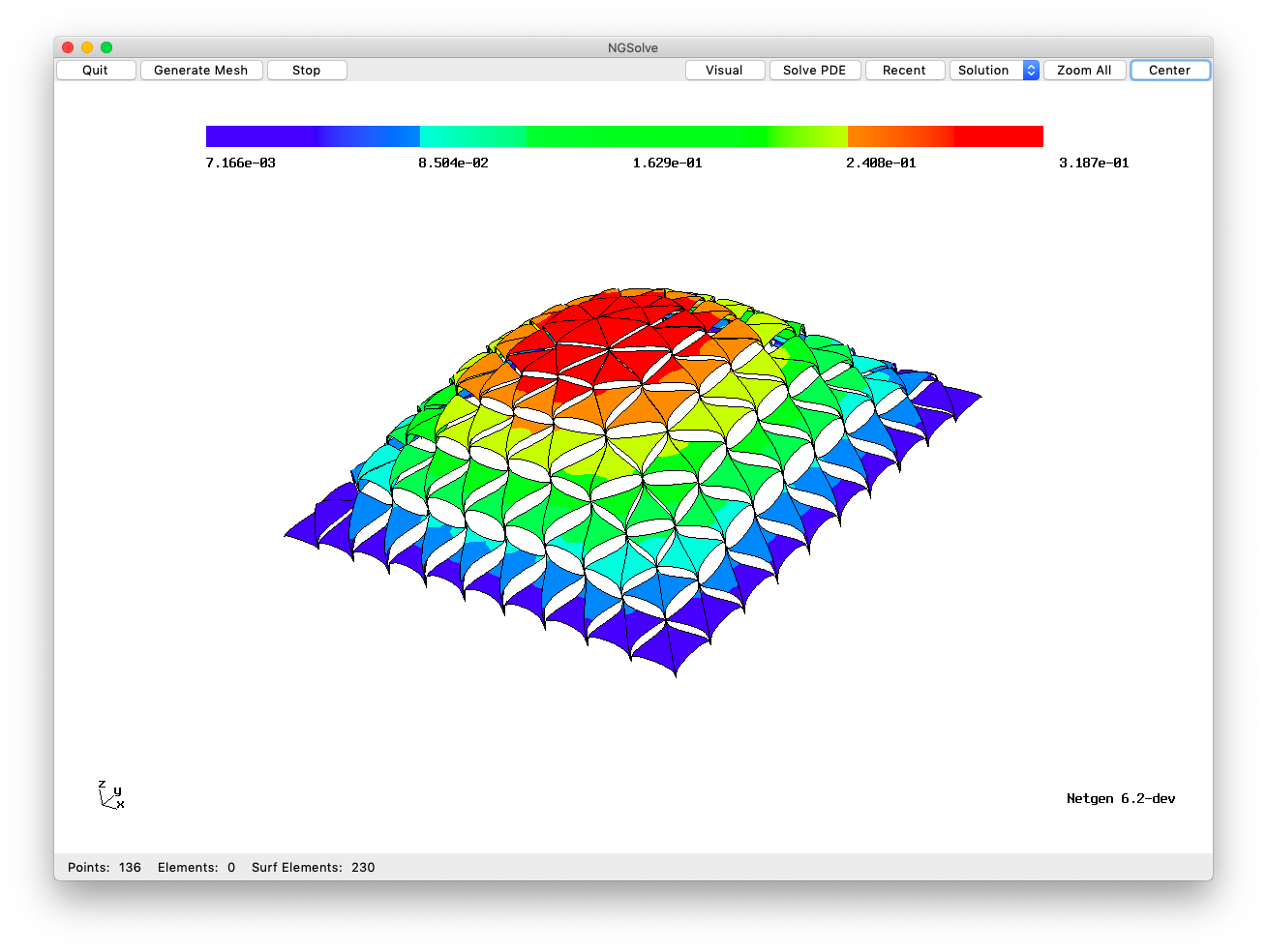
[1]:
import netgen.gui
from ngsolve import *
from ngsolve.la import EigenValues_Preconditioner
from netgen.csg import unit_cube
from netgen.geom2d import unit_square
SetHeapSize(100*1000*1000)
[2]:
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.5))
# mesh = Mesh(unit_square.GenerateMesh(maxh=0.5))
Built-in options¶
Let us define a simple function to study how the spectrum of the preconditioned matrix changes with various options.
Effect of condensation¶
[3]:
def TestPreconditioner (p, condense=False, **args):
fes = H1(mesh, order=p, **args)
u,v = fes.TnT()
a = BilinearForm(fes, eliminate_internal=condense)
a += grad(u)*grad(v)*dx + u*v*dx
c = Preconditioner(a, "bddc")
a.Assemble()
return EigenValues_Preconditioner(a.mat, c.mat)
[4]:
lams = TestPreconditioner(5)
print (lams[0:3], "...\n", lams[-3:])
1.0018
1.07103
1.24782
...
21.2736
22.7821
22.9382
Here is the effect of static condensation on the BDDC preconditioner.
[5]:
lams = TestPreconditioner(5, condense=True)
print (lams[0:3], "...\n", lams[-3:])
1.00026
1.03169
1.09454
...
4.10312
4.13286
4.24601
Tuning the auxiliary space¶
Next, let us study the effect of a few built-in flags for finite element spaces that are useful for tweaking the behavior of the BDDC preconditioner. The effect of these flags varies in two (2D) and three dimensions (3D), e.g.,
wb_fulledges=True: This option keeps all edge-dofs conforming (i.e. they are markedWIREBASKET_DOFs). This option is only meaningful in 3D. If used in 2D, the preconditioner becomes a direct solver.wb_withedges=True: This option keeps only the first edge-dof conforming (i.e., the first edge-dof is markedWIREBASKET_DOFand the remaining edge-dofs are markedINTERFACE_DOFs).
The complete situation is a bit more complex due to the fact these options can take the three values True, False, or Undefined, the two options can be combined, and the space dimension can be 2 or 3. The default value of these flags in NGSolve is Undefined. Here is a table with the summary of the effect of these options:
wb_fulledges |
wb_withedges |
2D |
3D |
|---|---|---|---|
True |
any value |
all |
all |
False/Undefined |
Undefined |
none |
first |
False/Undefined |
False |
none |
none |
False/Undefined |
True |
first |
first |
An entry \(X \in\) {all, none, first} of the last two columns is to be read as follows: \(X\) of the edge-dofs is(are) WIREBASKET_DOF(s).
Here is an example of the effect of one of these flag values.
[6]:
lams = TestPreconditioner(5, condense=True,
wb_withedges=False)
print (lams[0:3], "...\n", lams[-3:])
1.00121
1.0817
1.23231
...
25.7229
25.723
27.2163
Clearly, when moving from the default case (where the first of the edge dofs are wire basket dofs) to the case (where none of the edge dofs are wire basket dofs), the conditioning became less favorable.
Customize¶
From within python, we can change the types of degrees of freedom of finite element spaces, thus affecting the behavior of the BDDC preconditioner.
To depart from the default and commit the first two edge dofs to wire basket, we perform the next steps:
[7]:
fes = H1(mesh, order=10)
u,v = fes.TnT()
for ed in mesh.edges:
dofs = fes.GetDofNrs(ed)
for d in dofs:
fes.SetCouplingType(d, COUPLING_TYPE.INTERFACE_DOF)
# Set the first two edge dofs to be conforming
fes.SetCouplingType(dofs[0], COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(dofs[1], COUPLING_TYPE.WIREBASKET_DOF)
a = BilinearForm(fes, eliminate_internal=True)
a += grad(u)*grad(v)*dx + u*v*dx
c = Preconditioner(a, "bddc")
a.Assemble()
lams=EigenValues_Preconditioner(a.mat, c.mat)
max(lams)/min(lams)
[7]:
10.084234357497456
This is a slight improvement from the default.
[8]:
lams = TestPreconditioner (10, condense=True)
max(lams)/min(lams)
[8]:
14.092850105312214
Combine BDDC with AMG for large problems¶
coarsetype=h1amg flag, we can ask BDDC to replace \({\,\widetilde{A}\,}^{-1}\) by an Algebraic MultiGrid (AMG) preconditioner. Since NGSolve’s h1amg is well-suitedwb_withedges=False to ensure that \(\widetilde{A}\) is made solely with vertex unknowns.[9]:
p = 5
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.05))
fes = H1(mesh, order=p, dirichlet="left|bottom|back",
wb_withedges=False)
print("NDOF = ", fes.ndof)
u,v = fes.TnT()
a = BilinearForm(fes)
a += grad(u)*grad(v)*dx
f = LinearForm(fes)
f += v*dx
with TaskManager():
pre = Preconditioner(a, "bddc", coarsetype="h1amg")
a.Assemble()
f.Assemble()
gfu = GridFunction(fes)
solvers.CG(mat=a.mat, rhs=f.vec, sol=gfu.vec,
pre=pre, maxsteps=500)
Draw(gfu)
NDOF = 1113131
it = 0 err = 0.7050998115811555
it = 1 err = 0.2865027046238019
it = 2 err = 0.2672614246548547
it = 3 err = 0.27542043772095026
it = 4 err = 0.2914821787991746
it = 5 err = 0.22415324391099575
it = 6 err = 0.17197399516467127
it = 7 err = 0.13712707079606498
it = 8 err = 0.10848911838359887
it = 9 err = 0.08030186368382719
it = 10 err = 0.06032235038857111
it = 11 err = 0.047970608810490305
it = 12 err = 0.03816858395726897
it = 13 err = 0.03180612844818761
it = 14 err = 0.02545006745026688
it = 15 err = 0.01994717742876711
it = 16 err = 0.01556767544785493
it = 17 err = 0.012357198897318704
it = 18 err = 0.009930597430727986
it = 19 err = 0.007704247075079049
it = 20 err = 0.005952919078330116
it = 21 err = 0.004690706961890581
it = 22 err = 0.003794390641192048
it = 23 err = 0.003026966468750931
it = 24 err = 0.002382850279693516
it = 25 err = 0.0019262350508682728
it = 26 err = 0.0015475132964049806
it = 27 err = 0.0012358382215364387
it = 28 err = 0.0009733560696756669
it = 29 err = 0.0007743968754281993
it = 30 err = 0.0006217899463182861
it = 31 err = 0.000496605478930589
it = 32 err = 0.0003924413832723055
it = 33 err = 0.0003021982718858036
it = 34 err = 0.00023979710728981997
it = 35 err = 0.00019063569064363625
it = 36 err = 0.0001490423499025787
it = 37 err = 0.0001170005852187937
it = 38 err = 9.607116714898515e-05
it = 39 err = 7.741428770853819e-05
it = 40 err = 6.0102885489572097e-05
it = 41 err = 4.73097445994409e-05
it = 42 err = 3.8217331217617485e-05
it = 43 err = 3.052220014762531e-05
it = 44 err = 2.3982000565149712e-05
it = 45 err = 1.937390160506436e-05
it = 46 err = 1.5810111291839845e-05
it = 47 err = 1.273924385606073e-05
it = 48 err = 9.955033051126215e-06
it = 49 err = 7.875532076759112e-06
it = 50 err = 6.341533501757464e-06
it = 51 err = 5.08453246209007e-06
it = 52 err = 4.002976035385213e-06
it = 53 err = 3.2354098732121687e-06
it = 54 err = 2.6028624841701193e-06
it = 55 err = 2.047751562514492e-06
it = 56 err = 1.6220825417323527e-06
it = 57 err = 1.2980733619635255e-06
it = 58 err = 1.0384926648028402e-06
it = 59 err = 8.264226938466562e-07
it = 60 err = 6.580327496612792e-07
it = 61 err = 5.258101198314505e-07
it = 62 err = 4.251235686169375e-07
it = 63 err = 3.4157477029301453e-07
it = 64 err = 2.6705887857936325e-07
it = 65 err = 2.1023511660778804e-07
it = 66 err = 1.67528591155507e-07
it = 67 err = 1.3521781379750386e-07
it = 68 err = 1.0718907702655886e-07
it = 69 err = 8.516127806313479e-08
it = 70 err = 6.892931277400276e-08
it = 71 err = 5.517290367095728e-08
it = 72 err = 4.3507157987488137e-08
it = 73 err = 3.442313662651814e-08
it = 74 err = 2.7501679806321236e-08
it = 75 err = 2.1934879836980713e-08
it = 76 err = 1.744108813631586e-08
it = 77 err = 1.3749335959875282e-08
it = 78 err = 1.1026509626930305e-08
it = 79 err = 8.851598916705129e-09
it = 80 err = 6.995767147873586e-09
it = 81 err = 5.499927358902213e-09
it = 82 err = 4.376985003243652e-09
it = 83 err = 3.518243409712814e-09
it = 84 err = 2.8303272882225553e-09
it = 85 err = 2.277669792659171e-09
it = 86 err = 1.801726842307486e-09
it = 87 err = 1.4263990934524098e-09
it = 88 err = 1.1471933152823695e-09
it = 89 err = 9.162990426336366e-10
it = 90 err = 7.313781112835042e-10
it = 91 err = 5.752962873929444e-10
it = 92 err = 4.5993607363115635e-10
it = 93 err = 3.6582896620011495e-10
it = 94 err = 2.92949567502834e-10
it = 95 err = 2.3448332511202825e-10
it = 96 err = 1.8793903661743774e-10
it = 97 err = 1.5044186349118155e-10
it = 98 err = 1.1874245481453724e-10
it = 99 err = 9.392793596544757e-11
it = 100 err = 7.529552712421298e-11
it = 101 err = 5.998003416431769e-11
it = 102 err = 4.727299984440525e-11
it = 103 err = 3.7250642944548297e-11
it = 104 err = 2.9573374431657214e-11
it = 105 err = 2.350664871153587e-11
it = 106 err = 1.8670406996605795e-11
it = 107 err = 1.4798553333739112e-11
it = 108 err = 1.1670280177366993e-11
it = 109 err = 9.469825369786133e-12
it = 110 err = 7.622547657936367e-12
it = 111 err = 6.0374693878386846e-12
it = 112 err = 4.798578698089458e-12
it = 113 err = 3.780579425412057e-12
it = 114 err = 3.0187386236893005e-12
it = 115 err = 2.4046320299265e-12
it = 116 err = 1.9214333091700654e-12
it = 117 err = 1.520576418497056e-12
it = 118 err = 1.2059076586893695e-12
it = 119 err = 9.559364351639222e-13
it = 120 err = 7.567516205433916e-13
it = 121 err = 6.030468752570467e-13
Postscript¶
By popular demand, here is the code to draw the figure found at the beginning of this tutorial:
[10]:
from netgen.geom2d import unit_square
mesh = Mesh(unit_square.GenerateMesh(maxh=0.1))
fes_ho = Discontinuous(H1(mesh, order=10))
fes_lo = H1(mesh, order=1, dirichlet=".*")
fes_lam = Discontinuous(H1(mesh, order=1))
fes = FESpace([fes_ho, fes_lo, fes_lam])
uho, ulo, lam = fes.TrialFunction()
a = BilinearForm(fes)
a += Variation(0.5 * grad(uho)*grad(uho)*dx
- 1*uho*dx
+ (uho-ulo)*lam*dx(element_vb=BBND))
gfu = GridFunction(fes)
solvers.Newton(a=a, u=gfu)
Draw(gfu.components[0])
Newton iteration 0
err = 0.3929793997717295
Newton iteration 1
err = 6.621326119794413e-15