Poisson equation¶
We solve the Poisson equation on the unit-square, with homogeneous Dirichlet boundary conditions. You can run the example either directly within the Python interpreter (Python version 3 is required!):
python3 poisson.py
or you can run it with Netgen providing you also a graphical user interface
netgen poisson.py
# solve the Poisson equation -Delta u = f
# with Dirichlet boundary condition u = 0
from ngsolve import *
from netgen.geom2d import unit_square
ngsglobals.msg_level = 1
# generate a triangular mesh of mesh-size 0.2
mesh = Mesh (unit_square.GenerateMesh(maxh=0.2))
# H1-conforming finite element space
V = H1(mesh, order=3, dirichlet=[1,2,3,4])
# the right hand side
f = LinearForm (V)
f += Source (32 * (y*(1-y)+x*(1-x)))
# the bilinear-form
a = BilinearForm (V, symmetric=False)
a += Laplace (1)
a.Assemble()
f.Assemble()
# the solution field
u = GridFunction (V)
u.vec.data = a.mat.Inverse(V.FreeDofs(), inverse="sparsecholesky") * f.vec
# print (u.vec)
# plot the solution (netgen-gui only)
Draw (u)
Draw (-u.Deriv(), mesh, "Flux")
exact = 16*x*(1-x)*y*(1-y)
print ("L2-error:", sqrt (Integrate ( (u-exact)*(u-exact), mesh)))
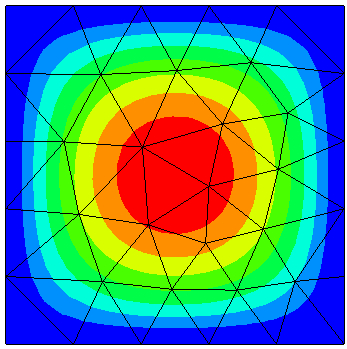
The solution visualized in Netgen: