Periodicity¶

Netgen is able to create periodic meshes, with them NGSolve can create periodic finite element spaces by mapping the degrees of freedom on the slave boundary to the ones on the master boundary. To use this functionality create a periodic mesh first:

Periodic Meshes¶

3D¶

If a geometry object has a periodic identification, Netgen creates a periodic mesh for the specified surfaces. In 3 dimensions, this identification is created using CSGeometry.PeriodicSurfaces(master,slave). Here we define a cube with periodicity in x-direction and create a periodic NGSolve mesh for it:

from netgen.csg import *

geo = CSGeometry()
left = Plane(Pnt(0,0,0),Vec(-1,0,0))
right = Plane(Pnt(1,0,0),Vec(1,0,0))
brick = OrthoBrick(Pnt(-1,0,0),Pnt(2,1,1)).bc("outer")
cube = brick * left * right
geo.Add(cube)
geo.PeriodicSurfaces(left,right)

from ngsolve import *
mesh = Mesh(geo.GenerateMesh(maxh=0.3))

2D¶

In two dimensions you can create periodic geometries with the copy parameter of the SplineGeometry.Append method. This defines the appended spline as the slave of the one given in copy:

Caution

The slave boundaries must be defined in the same direction as the master ones!

from netgen.geom2d import *

periodic = SplineGeometry()
pnts = [ (0,0), (1,0), (1,1), (0,1) ]
pnums = [periodic.AppendPoint(*p) for p in pnts]

periodic.Append ( ["line", pnums[0], pnums[1]],bc="outer")
# This should be our master edge so we need to save its number.
lright = periodic.Append ( ["line", pnums[1], pnums[2]], bc="periodic")
periodic.Append ( ["line", pnums[2], pnums[3]], bc="outer")
# Slave boundaries must be defined in the same direction as master ones,
# this is why the the point numbers of this spline are defined in the reverse direction,
# leftdomain and rightdomain must therefore be switched as well!
# We use the master number as the copy argument to create a slave edge.
periodic.Append ( ["line", pnums[0], pnums[3]], leftdomain=0, rightdomain=1, copy=lright, bc="periodic")

from ngsolve import *
mesh = Mesh(periodic.GenerateMesh(maxh=0.2))

1D¶

In one dimension you can add periodic identifications to points (This is not necessary for mesh creation of course, but lets NGSolve find the periodic vertices the same way as it finds the ones in higher dimensions). The added point numbers must be the ones returned from mesh.Add(MeshPoint). This is a manually created mesh with periodic boundaries:

from netgen.meshing import *

mesh = Mesh(dim=1)
pids = []
n = 50
for i in range(n+1):
    pids.append (mesh.Add (MeshPoint(Pnt(i/n, 0, 0))))
for i in range(n):
    mesh.Add(Element1D([pids[i],pids[i+1]],index=1))
mesh.Add (Element0D( pids[0], index=1))
mesh.Add (Element0D( pids[n], index=2))
mesh.AddPointIdentification(pids[0],pids[n],1,2)

Periodic FESpace¶

The periodic finite element space is created using the generator function Periodic. A quasi-periodic space can be created the same way if the optional parameter ‘phase’ is set.

Caution

The phase shifts must be given in the same order as the definition of the periodic boundaries in the geometry!

We can solve a periodic problem using the above defined mesh:

fes = Periodic(H1(mesh,order=3,dirichlet="outer"))

u,v = fes.TrialFunction(), fes.TestFunction()

a = BilinearForm(fes,symmetric=True)
a += SymbolicBFI(grad(u) * grad(v))

f = LinearForm(fes)
f += SymbolicLFI(x*v)

u = GridFunction(fes,"u")

with TaskManager():
    a.Assemble()
    f.Assemble()
    u.vec.data = a.mat.Inverse(fes.FreeDofs()) * f.vec

Draw(u)

The solution of this problem plotted in 2D and in 3D:

You can download these examples here: 1D, 2D, 3D.

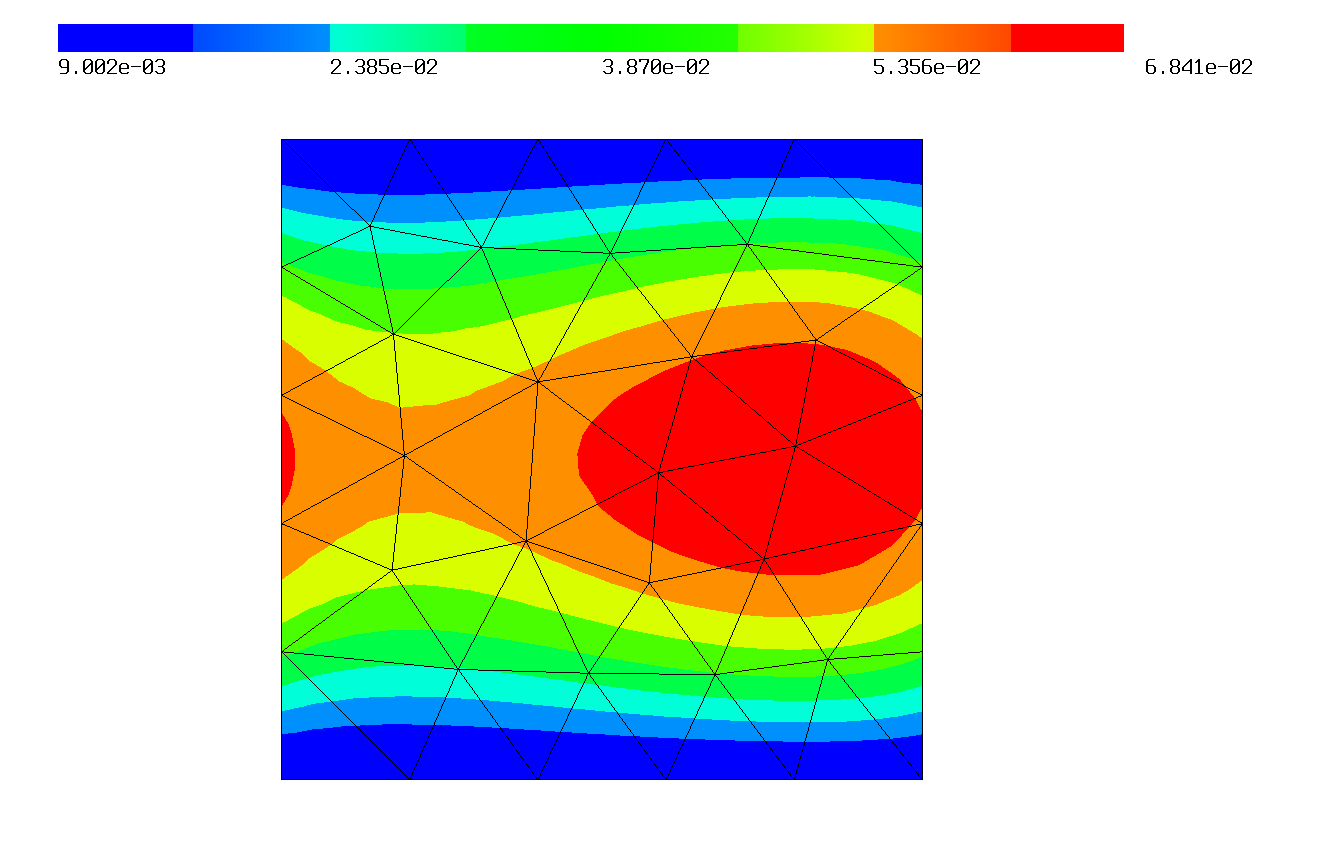
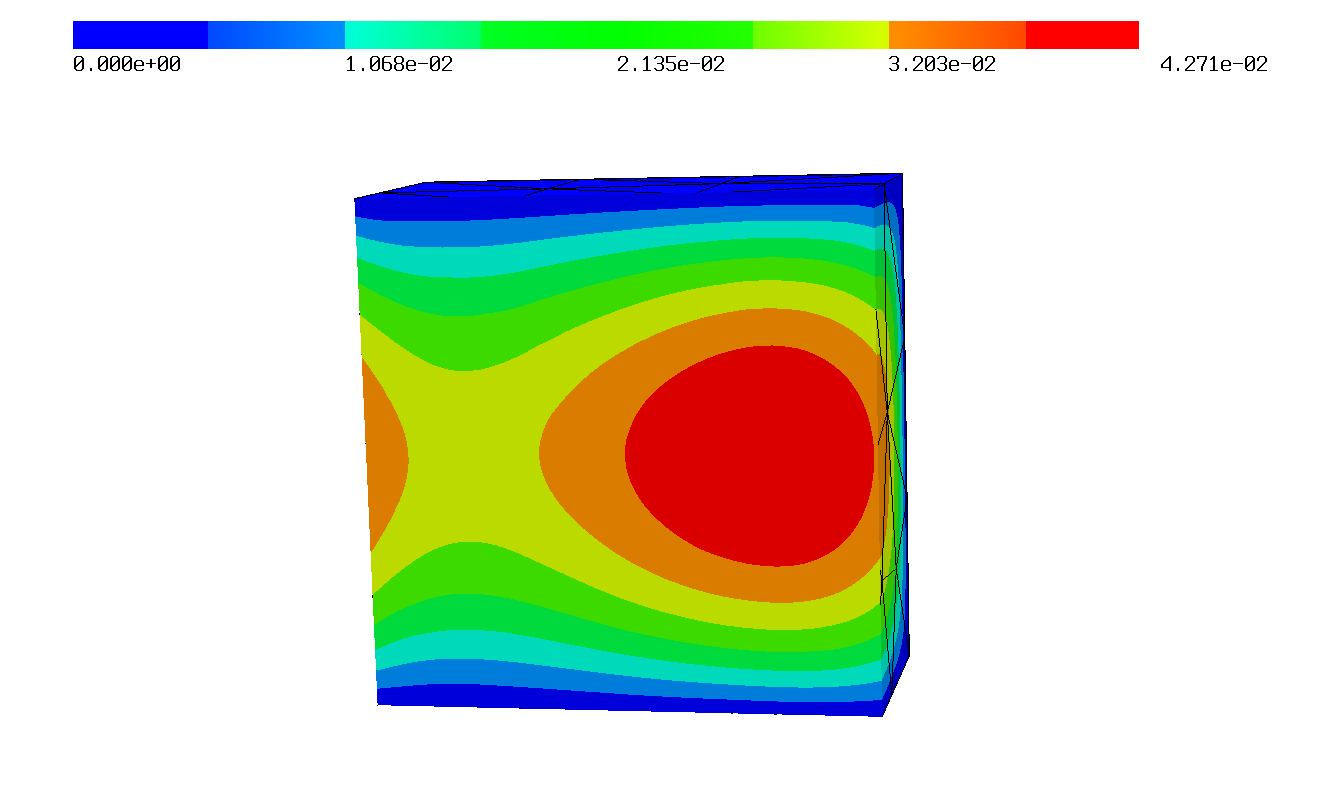
Function Documentation¶

ngsolve.Periodic(fespace: ngsolve.comp.FESpace, phase: object=<ngsolve.ngstd.DummyArgument>, use_idnrs: object=[]) → ngsolve.comp.FESpace¶

Generator function for periodic or quasi-periodic Finite Element Spaces. The periodic fespace is a wrapper around a standard fespace with an additional dof mapping for the periodic degrees of freedom. All dofs on slave boundaries are mapped to their master dofs. Because of this, the mesh needs to be periodic. Low order fespaces are currently not supported, so methods using them will not work.

Parameters:

fespace: finite element space
phase: phase shift for quasi-periodic finite element space. The basis functions on the slave boundary are multiplied by the factor given in this list. If None (default) is given, a periodic fespace is created. The order of the list must match the order of the definition of the periodic boundaries in the mesh.
used_idnrs: identification numbers to be made periodic if you don’t want to use all periodic identifications defined in the mesh, if None (default) all available periodic identifications are used.