This page was generated from unit-6.1.3-rmplate/Reissner_Mindlin_plate.ipynb.

6.1.3 Reissner-Mindlin plate

To avoid shear locking when the thickness \(t\) becomes small several methods and elements have been proposed. We discuss two approaches:

1: Mixed Interpolation of Tensorial Components (MITC)

2: Rotations in Nèdèlec space using the Tangential-Displacement Normal-Normal-Stress method (TDNNS)

Mixed Interpolation of Tensorial Components (MITC)

from ngsolve import *
from netgen.geom2d import SplineGeometry
from ngsolve.webgui import Draw

Set up benchmark example with exact solution. Young modulus \(E\), Poisson ratio \(\nu\), shear correction factor \(\kappa\) and corresponding Lamè parameters \(\mu\) and \(\lambda\). Geometry parameters are given by thickness \(t\) and radius \(R\).

E, nu, k = 10.92, 0.3, 5/6
mu  = E/(2*(1+nu))
lam = E*nu/(1-nu**2)
#shearing modulus
G = E/(2*(1+nu))
#thickness, shear locking with t=0.1
t = 0.1
R = 5
#force
fz = 1

order = 1

Due to symmetry we only need to mesh one quarter of the circle.

sg = SplineGeometry()
pnts = [ (0,0), (R,0), (R,R), (0,R) ]
pind = [ sg.AppendPoint(*pnt) for pnt in pnts ]
sg.Append(['line',pind[0],pind[1]], leftdomain=1, rightdomain=0, bc="bottom")
sg.Append(['spline3',pind[1],pind[2],pind[3]], leftdomain=1, rightdomain=0, bc="circ")
sg.Append(['line',pind[3],pind[0]], leftdomain=1, rightdomain=0, bc="left")
mesh = Mesh(sg.GenerateMesh(maxh=R/3))
mesh.Curve(order)
Draw(mesh)

 Generate Mesh from spline geometry
 Boundary mesh done, np = 11
 CalcLocalH: 11 Points 0 Elements 0 Surface Elements
 Meshing domain 1 / 1
 load internal triangle rules
 Surface meshing done
 Edgeswapping, topological
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Update mesh topology
 Update clusters
 Curve elements, order = 1
 Update clusters

BaseWebGuiScene

Depending on the boundary conditions (simply supported or clamped) we have different exact solutions for the vertical displacement.

r = sqrt(x**2+y**2)
xi = r/R
Db = E*t**3/(12*(1-nu**2))

clamped = True

#exact solution for simply supported bc
w_s_ex = -fz*R**4/(64*Db)*(1-xi**2)*( (6+2*nu)/(1+nu) - (1+xi**2) + 8*(t/R)**2/(3*k*(1-nu)))
#Draw(w_s_ex, mesh, "w_s_ex")
#exact solution for clamped bc
w_c_ex = -fz*R**4/(64*Db)*(1-xi**2)*( (1-xi**2) + 8*(t/R)**2/(3*k*(1-nu)))
Draw(w_c_ex, mesh, "w_c_ex")

BaseWebGuiScene

Use (lowest order) Lagrangian finite elements for rotations and the vertical deflection together with additional internal bubbles for order >1.

if clamped:
    fesB = VectorH1(mesh, order=order, orderinner=order+1, dirichletx="circ|left", dirichlety="circ|bottom", autoupdate=True)
else:
    fesB = VectorH1(mesh, order=order, orderinner=order+1, dirichletx="left", dirichlety="bottom", autoupdate=True)
fesW = H1(mesh, order=order, orderinner=order+1, dirichlet="circ", autoupdate=True)
fes = FESpace( [fesB, fesW], autoupdate=True )
(beta,u), (dbeta,du) = fes.TnT()

WARNING: kwarg 'orderinner' is an undocumented flags option for class <class 'ngsolve.comp.VectorH1'>, maybe there is a typo?
WARNING: kwarg 'orderinner' is an undocumented flags option for class <class 'ngsolve.comp.H1'>, maybe there is a typo?
WARNING: kwarg 'autoupdate' is an undocumented flags option for class <class 'ngsolve.comp.FESpace'>, maybe there is a typo?

Direct approach where shear locking may occur

\[\frac{t^3}{12}\int_{\Omega} 2\mu\, \varepsilon(\beta):\varepsilon(\delta\beta) + \lambda\, \text{div}(\beta)\text{div}(\delta\beta)\,dx + t\kappa\,G\int_{\Omega}(\nabla u-\beta)\cdot(\nabla\delta u-\delta\beta)\,dx = \int_{\Omega} f\,\delta u\,dx,\qquad \forall (\delta u,\delta\beta).\]

Adding interpolation (reduction) operator \(\boldsymbol{R}:[H^1_0(\Omega)]^2\to H(\text{curl})\). Spaces are chosen according to [Brezzi, Fortin and Stenberg. Error analysis of mixed-interpolated elements for Reissner-Mindlin plates. Mathematical Models and Methods in Applied Sciences 1, 2 (1991), 125-151.]

\[\frac{t^3}{12}\int_{\Omega} 2\mu\, \varepsilon(\beta):\varepsilon(\delta\beta) + \lambda\, \text{div}(\beta)\text{div}(\delta\beta)\,dx + t\kappa\,G\int_{\Omega}\boldsymbol{R}(\nabla u-\beta)\cdot\boldsymbol{R}(\nabla\delta u-\delta\beta)\,dx = \int_{\Omega} f\,\delta u\,dx,\qquad \forall (\delta u,\delta\beta).\]

Gamma = HCurl(mesh,order=order,orderedge=order-1, autoupdate=True)

a = BilinearForm(fes)
a += t**3/12*(2*mu*InnerProduct(Sym(grad(beta)),Sym(grad(dbeta))) + lam*div(beta)*div(dbeta))*dx
#a += t*k*G*InnerProduct( grad(u)-beta, grad(du)-dbeta )*dx
a += t*k*G*InnerProduct(Interpolate(grad(u)-beta,Gamma), Interpolate(grad(du)-dbeta,Gamma))*dx

f = LinearForm(fes)
f += -fz*du*dx

gfsol = GridFunction(fes, autoupdate=True)
gfbeta, gfu = gfsol.components

WARNING: kwarg 'orderedge' is an undocumented flags option for class <class 'ngsolve.comp.HCurl'>, maybe there is a typo?

Define function for solving the problem.

def SolveBVP():
    fes.Update()
    gfsol.Update()
    with TaskManager():
        a.Assemble()
        f.Assemble()
        inv = a.mat.Inverse(fes.FreeDofs(), inverse="sparsecholesky")
        gfsol.vec.data = inv * f.vec

Solve, compute error, refine, …

l = []
for i in range(5):
    print("i = ", i)
    SolveBVP()
    if clamped:
        norm_w = sqrt(Integrate(w_c_ex*w_c_ex, mesh))
        err = sqrt(Integrate((gfu-w_c_ex)*(gfu-w_c_ex), mesh))/norm_w
    else:
        norm_w = sqrt(Integrate(w_s_ex*w_s_ex, mesh))
        err = sqrt(Integrate((gfu-w_s_ex)*(gfu-w_s_ex), mesh))/norm_w
    print("err = ", err)
    l.append ( (fes.ndof, err ))
    mesh.Refine()

i =  0
assemble VOL element 13/13
assemble VOL element 13/13
err =  0.5595598334579744
 Mesh bisection
 resetting marked-element information
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  1
assemble VOL element 52/52
assemble VOL element 52/52
err =  0.11654484017074333
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  2
assemble VOL element 208/208
assemble VOL element 208/208
err =  0.021448789398276467
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  3
assemble VOL element 832/832
assemble VOL element 832/832
err =  0.004856535560784435
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  4
assemble VOL element 3328/3328
assemble VOL element 3328/3328
err =  0.001174815886210361
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters

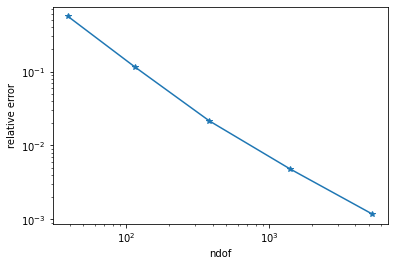
Convergence plot with matplotlib.

import matplotlib.pyplot as plt

plt.yscale('log')
plt.xscale('log')
plt.xlabel("ndof")
plt.ylabel("relative error")
ndof,err = zip(*l)
plt.plot(ndof,err, "-*")
plt.ion()
plt.show()

TDNNS method

Invert material law of Hooke and reset mesh.

def CMatInv(mat, E, nu):
    return (1+nu)/E*(mat-nu/(nu+1)*Trace(mat)*Id(2))

mesh = Mesh(sg.GenerateMesh(maxh=R/3))
mesh.Curve(order)
Draw(mesh)

 Generate Mesh from spline geometry
 Boundary mesh done, np = 11
 CalcLocalH: 11 Points 0 Elements 0 Surface Elements
 Meshing domain 1 / 1
 Surface meshing done
 Edgeswapping, topological
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Edgeswapping, metric
 Smoothing
 Split improve
 Combine improve
 Smoothing
 Update mesh topology
 Update clusters
 Curve elements, order = 1
 Update clusters

BaseWebGuiScene

Instead of using Lagrangian elements together with an interpolation operator we can directly use H(curl) for the roation \(\beta\).

order=1
if clamped:
    fesB = HCurl(mesh, order=order-1, dirichlet="circ", autoupdate=True)
    fesS = HDivDiv(mesh, order=order-1, dirichlet="", autoupdate=True)
else:
    fesB = HCurl(mesh, order=order-1)
    fesS = HDivDiv(mesh, order=order-1, dirichlet="circ", autoupdate=True)
fesW = H1(mesh, order=order, dirichlet="circ", autoupdate=True)

fes = FESpace( [fesW, fesB, fesS], autoupdate=True )
(u,beta,sigma), (du,dbeta,dsigma) = fes.TnT()

WARNING: kwarg 'autoupdate' is an undocumented flags option for class <class 'ngsolve.comp.FESpace'>, maybe there is a typo?

Use the TDNNS method with the stress (bending) tensor \(\boldsymbol{\sigma}\) as proposed in [Pechstein and Schöberl. The TDNNS method for Reissner-Mindlin plates. Numerische Mathematik 137, 3 (2017), 713-740] \begin{align*} &\mathcal{L}(u,\beta,\boldsymbol{\sigma})=-\frac{6}{t^3}\|\boldsymbol{\sigma}\|^2_{\mathcal{C}^{-1}} + \langle \boldsymbol{\sigma}, \nabla \beta\rangle + \frac{tkG}{2}\|\nabla u-\beta\|^2 -\int_{\Omega} f\cdot u\,dx\\ &\langle \boldsymbol{\sigma}, \nabla \beta\rangle:= \sum_{T\in\mathcal{T}}\int_T\boldsymbol{\sigma}:\nabla \beta\,dx -\int_{\partial T}\boldsymbol{\sigma}_{nn}\beta_n\,ds \end{align*}

n = specialcf.normal(2)

a = BilinearForm(fes)
a += (-12/t**3*InnerProduct(CMatInv(sigma, E, nu),dsigma) + InnerProduct(dsigma,grad(beta)) + InnerProduct(sigma,grad(dbeta)))*dx
a += ( -((sigma*n)*n)*(dbeta*n) - ((dsigma*n)*n)*(beta*n) )*dx(element_boundary=True)
a += t*k*G*InnerProduct( grad(u)-beta, grad(du)-dbeta )*dx

f = LinearForm(fes)
f += -fz*du*dx

gfsol = GridFunction(fes, autoupdate=True)
gfu, gfbeta, gfsigma = gfsol.components

def SolveBVP():
    fes.Update()
    gfsol.Update()
    with TaskManager():
        a.Assemble()
        f.Assemble()
        inv = a.mat.Inverse(fes.FreeDofs())
        gfsol.vec.data = inv * f.vec

Solve, compute error, and refine.

l = []
for i in range(5):
    print("i = ", i)
    SolveBVP()
    if clamped:
        norm_w = sqrt(Integrate(w_c_ex*w_c_ex, mesh))
        err = sqrt(Integrate((gfu-w_c_ex)*(gfu-w_c_ex), mesh))/norm_w
    else:
        norm_w = sqrt(Integrate(w_s_ex*w_s_ex, mesh))
        err = sqrt(Integrate((gfu-w_s_ex)*(gfu-w_s_ex), mesh))/norm_w
    print("err = ", err)
    l.append ( (fes.ndof, err ))
    mesh.Refine()

i =  0
assemble VOL element 13/13
assemble VOL element 13/13
call pardiso ... done
err =  0.4806915268060298
 Mesh bisection
 resetting marked-element information
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  1
assemble VOL element 52/52
assemble VOL element 52/52
call pardiso ... done
err =  0.1660840390786989
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  2
assemble VOL element 208/208
assemble VOL element 208/208
call pardiso ... done
err =  0.04302102327870844
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  3
assemble VOL element 832/832
assemble VOL element 832/832
call pardiso ... done
err =  0.011002228686409238
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters
i =  4
assemble VOL element 3328/3328
assemble VOL element 3328/3328
call pardiso ... done
err =  0.0028879335138407747
 Mesh bisection
 Update mesh topology
 Update clusters
 Bisection done
 Update clusters

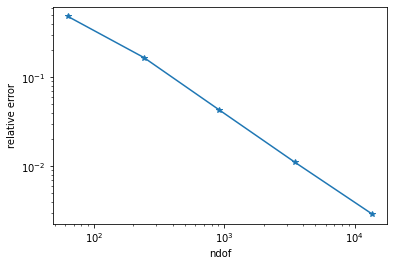
Convergence plot with matplotlib.

plt.yscale('log')
plt.xscale('log')
plt.xlabel("ndof")
plt.ylabel("relative error")
ndof,err = zip(*l)
plt.plot(ndof,err, "-*")

plt.ion()
plt.show()