This page was generated from wta/adaptivity.ipynb.
Adaptivity¶
[1]:
from ngsolve import *
from ngsolve.webgui import Draw
from netgen.geom2d import SplineGeometry
Define a geometry by curves:
[2]:
# point numbers 0, 1, ... 11
# sub-domain numbers (1), (2), (3)
#
#
# 7-------------6
# | |
# | (2) |
# | |
# 3------4-------------5------2
# | |
# | 11 |
# | / \ |
# | 10 (3) 9 |
# | \ / (1) |
# | 8 |
# | |
# 0---------------------------1
#
def MakeGeometry():
geometry = SplineGeometry()
# point coordinates ...
pnts = [ (0,0), (1,0), (1,0.6), (0,0.6), \
(0.2,0.6), (0.8,0.6), (0.8,0.8), (0.2,0.8), \
(0.5,0.15), (0.65,0.3), (0.5,0.45), (0.35,0.3) ]
pnums = [geometry.AppendPoint(*p) for p in pnts]
# start-point, end-point, boundary-condition, left-domain, right-domain:
lines = [ (0,1,"bot",1,0), (1,2,"outer",1,0), (2,5,"outer",1,0), (5,4,"inner",1,2), (4,3,"outer",1,0), (3,0,"outer",1,0), \
(5,6,"outer",2,0), (6,7,"outer",2,0), (7,4,"outer",2,0), \
(8,9,"inner",3,1), (9,10,"inner",3,1), (10,11,"inner",3,1), (11,8,"inner",3,1) ]
for p1,p2,bc,left,right in lines:
geometry.Append(["line", pnums[p1], pnums[p2]], bc=bc, leftdomain=left, rightdomain=right)
geometry.SetMaterial(1,"base")
geometry.SetMaterial(2,"top")
geometry.SetMaterial(3,"chip")
return geometry
geo = MakeGeometry()
# Draw(geo)
Piece-wise constant coefficients in sub-domains:
[3]:
mesh = Mesh(geo.GenerateMesh(maxh=0.2))
fes = H1(mesh, order=3, dirichlet="bot", autoupdate=True)
u, v = fes.TnT()
lam = CoefficientFunction([1, 1000, 10])
a = BilinearForm(fes)
a += lam*grad(u)*grad(v)*dx
# heat-source in inner subdomain
f = LinearForm(fes)
f += 1*v*dx(definedon="chip")
c = Preconditioner(a, type="multigrid", inverse="sparsecholesky")
gfu = GridFunction(fes, autoupdate=True)
Assemble and solve problem:
[4]:
def SolveBVP():
a.Assemble()
f.Assemble()
inv = CGSolver(a.mat, c.mat)
gfu.vec.data = inv * f.vec
SolveBVP()
Draw (gfu, mesh)
[4]:
Gradient recovery error estimator: Interpolate finite element flux
\[q_h := I_h (\lambda \nabla u_h)\]
and take difference as element error indicator:
\[\eta_T := \tfrac{1}{\lambda} \| q_h - \lambda \nabla u_h \|_{L_2(T)}^2\]
[5]:
l = [] # l = list of estimated total error
space_flux = HDiv(mesh, order=2, autoupdate=True)
gf_flux = GridFunction(space_flux, "flux", autoupdate=True)
def CalcError():
# FEM-flux
flux = lam * grad(gfu)
# interpolate into H(div)
gf_flux.Set(flux)
# compute estimator:
err = 1/lam*(flux-gf_flux)*(flux-gf_flux)
eta2 = Integrate(err, mesh, VOL, element_wise=True)
l.append ((fes.ndof, sqrt(sum(eta2))))
print("ndof =", fes.ndof, " toterr =", sqrt(sum(eta2)))
# mark for refinement:
maxerr = max(eta2)
for el in mesh.Elements():
mesh.SetRefinementFlag(el, eta2[el.nr] > 0.25*maxerr)
CalcError()
ndof = 208 toterr = 0.0047861835772394345
Adaptive loop:
[6]:
level = 0
while fes.ndof < 50000:
mesh.Refine()
SolveBVP()
CalcError()
level = level+1
if level%5 == 0:
Draw (gfu)
ndof = 454 toterr = 0.0036081508491322767
ndof = 547 toterr = 0.00298640856132942
ndof = 1168 toterr = 0.0020124591768726978
ndof = 1984 toterr = 0.0012753055579924723
ndof = 2890 toterr = 0.00079999431345231
ndof = 3760 toterr = 0.0005088041990863703
ndof = 4567 toterr = 0.00033195353309517956
ndof = 5176 toterr = 0.00023705580873543416
ndof = 5821 toterr = 0.00017331742431486288
ndof = 6493 toterr = 0.00012667678504606463
ndof = 7120 toterr = 0.00010246756794702991
ndof = 7828 toterr = 7.662553021211018e-05
ndof = 8623 toterr = 6.105228957004535e-05
ndof = 9478 toterr = 4.6717580837295436e-05
ndof = 10426 toterr = 3.6787057506364205e-05
ndof = 11533 toterr = 2.915979909020063e-05
ndof = 12796 toterr = 2.4079046532738943e-05
ndof = 14356 toterr = 1.908780843721877e-05
ndof = 16321 toterr = 1.5036749761586e-05
ndof = 18976 toterr = 1.1511866941214884e-05
ndof = 21676 toterr = 9.043238592102235e-06
ndof = 25231 toterr = 6.843042535399151e-06
ndof = 28792 toterr = 5.400326682200678e-06
ndof = 33070 toterr = 4.250477494322207e-06
ndof = 39082 toterr = 3.230406570526318e-06
ndof = 45721 toterr = 2.461487672233459e-06
ndof = 52705 toterr = 1.9366962587297432e-06
[7]:
Draw (gfu)
[7]:
[8]:
%matplotlib inline
import matplotlib.pyplot as plt
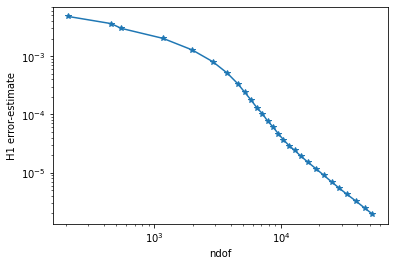
plt.yscale('log')
plt.xscale('log')
plt.xlabel("ndof")
plt.ylabel("H1 error-estimate")
ndof,err = zip(*l)
plt.plot(ndof,err, "-*")
plt.ion()
plt.show();
[ ]:
[ ]: