2.1.1 Preconditioners in NGSolve¶
Preconditioners are approximate inverses which are used within iterative methods to solve linear or non-linear equations.
Here are some built-in preconditioners in NGSolve:
- Jacobi and Block-Jacobi
- Direct solvers, i.e. sparse factorization
- Multigrid with different block-smoothers
- p-version element-level BDDC
This tutorial quickly introduces how to use these within a solver. (In later tutorials, we will see how to measure condition numbers and customize preconditioners.)
In [1]:
from netgen.csg import unit_cube
from netgen.geom2d import unit_square
from ngsolve import *
import netgen.gui
%gui tk
import matplotlib.pyplot as plt
A simple test problem¶
We define a simple Poisson problem solver with the name of a preconditioner as argument in order to experiment with preconditioners.
In [2]:
def SolveProblem(h=0.5, p=1, levels=1,
condense = False,
precond="local"):
"""
Solve Poisson problem on l refinement levels.
h: coarse mesh size
p: polynomial degree
l: number of refinement levels
precond: name of a built-in preconditioner
condense: if true, perform static condensations
OUTPUT:
List of tuples of ndofs and iterations
"""
mesh = Mesh(unit_square.GenerateMesh(maxh=h))
# mesh = Mesh(unit_cube.GenerateMesh(maxh=h))
fes = H1(mesh, order=p, dirichlet="bottom|left")
u, v = fes.TnT()
a = BilinearForm(fes, eliminate_internal=condense)
a += SymbolicBFI(grad(u)*(grad(v)))
f = LinearForm(fes)
f += SymbolicLFI(1*v)
gfu = GridFunction(fes)
Draw (gfu)
c = Preconditioner(a, precond) # 'Register' c to a BEFORE assembly
steps = []
for l in range(levels):
if l > 0: mesh.Refine()
fes.Update()
a.Assemble()
f.Assemble()
gfu.Update()
# Conjugate gradient solver
inv = CGSolver(a.mat, c.mat, maxsteps=1000)
# Solve steps depend on condense
if condense:
f.vec.data += a.harmonic_extension_trans * f.vec
gfu.vec.data = inv * f.vec
if condense:
gfu.vec.data += a.harmonic_extension * gfu.vec
gfu.vec.data += a.inner_solve * f.vec
steps.append ( (fes.ndof, inv.GetSteps()) )
Redraw ()
return steps
The Preconditioner registers itself to the BilinearForm.
Whenever the BilinearForm is re-assembled, the Preconditioner is
updated as well.
The local preconditioner¶
The local preconditioner is a simple Jacobi preconditioner. The
number of CG-iterations with the local preconditioner is proportional to
\(h^{-1} \sim 2^l\):
In [3]:
SolveProblem(precond="local")
Out[3]:
[(8, 4)]
In [4]:
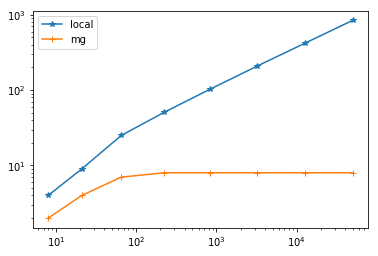
res_local = SolveProblem(levels=8, precond="local")
res_local
Out[4]:
[(8, 4),
(21, 9),
(65, 25),
(225, 51),
(833, 103),
(3201, 208),
(12545, 418),
(49665, 842)]
Multigrid preconditioner¶
A geometric multigrid Preconditioner uses the sequence of refined
meshes to define a preconditioner of optimal iteration number (and
complexity as well). It uses a direct solve on the coarsest level, and
block Gauss-Seidel smoothers on the refined levels
In [5]:
res_mg = SolveProblem(levels=8, precond="multigrid")
res_mg
Out[5]:
[(8, 2),
(21, 4),
(65, 7),
(225, 8),
(833, 8),
(3201, 8),
(12545, 8),
(49665, 8)]
In [6]:
plt.xscale("log")
plt.yscale("log")
plt.plot(*zip(*res_local), "-*")
plt.plot(*zip(*res_mg), "-+")
plt.legend(['local', 'mg'])
plt.show()
Multigrid implementation for higher order spaces¶
For high order elements we use hierarchical spaces, where the (small) sub-spaces \(V_E\), \(V_F\), and \(V_C\) are generated by basis functions associated with edges, faces, and cells:
The system matrix is stored as
The \(A_{VV}\)-block is exactly the system matrix of a lowest order method.
NGSolve’s multigrid implementation for a high order method uses h-version multigrid for the lowest order block, and local block-smoothing for the high order bubble basis functions.
In [7]:
for p in range(1,10):
r = SolveProblem(h=0.5, p=p, levels=4, condense=False,
precond="multigrid")
print ("p =",p,", res =",r)
p = 1 , res = [(8, 2), (21, 4), (65, 7), (225, 8)]
p = 2 , res = [(21, 5), (65, 6), (225, 8), (833, 8)]
p = 3 , res = [(40, 9), (133, 12), (481, 12), (1825, 13)]
p = 4 , res = [(65, 12), (225, 15), (833, 16), (3201, 16)]
p = 5 , res = [(96, 14), (341, 19), (1281, 20), (4961, 20)]
p = 6 , res = [(133, 16), (481, 23), (1825, 23), (7105, 23)]
p = 7 , res = [(176, 18), (645, 25), (2465, 26), (9633, 26)]
p = 8 , res = [(225, 19), (833, 27), (3201, 28), (12545, 28)]
p = 9 , res = [(280, 20), (1045, 29), (4033, 30), (15841, 30)]
We observe that the number of iterations grows mildly with the order, and remains bounded with mesh refinement.
Performing static condensation improves the situation:
In [8]:
for p in range(1,10):
r = SolveProblem(h=0.5, p=p, levels=4, condense=True,
precond="multigrid")
print ("p =",p,", res =",r)
p = 1 , res = [(8, 2), (21, 4), (65, 7), (225, 8)]
p = 2 , res = [(21, 5), (65, 6), (225, 8), (833, 8)]
p = 3 , res = [(40, 5), (133, 6), (481, 7), (1825, 8)]
p = 4 , res = [(65, 5), (225, 6), (833, 7), (3201, 8)]
p = 5 , res = [(96, 5), (341, 6), (1281, 7), (4961, 8)]
p = 6 , res = [(133, 5), (481, 6), (1825, 7), (7105, 8)]
p = 7 , res = [(176, 5), (645, 6), (2465, 7), (9633, 8)]
p = 8 , res = [(225, 5), (833, 6), (3201, 7), (12545, 8)]
p = 9 , res = [(280, 5), (1045, 6), (4033, 7), (15841, 8)]
Element-wise BDDC preconditioner¶
A built-in element-wise BDDC (Balancing Domain
Decomposition preconditioner with Constraints)
preconditioner is also available. In contrast to local or multigrid
preconditioners, the BDDC preconditioner needs access to the element
matrices. This is exactly the reason why we register the preconditioner
with the BilinerForm, and call the bfa.Assemble() later.
In [9]:
for p in range(1,10):
r = SolveProblem(h=0.25, p=p, levels=3, condense=True,
precond="bddc")
print ("p =",p,", res =",r)
p = 1 , res = [(27, 2), (89, 2), (321, 2)]
p = 2 , res = [(89, 14), (321, 19), (1217, 20)]
p = 3 , res = [(187, 18), (697, 23), (2689, 24)]
p = 4 , res = [(321, 21), (1217, 28), (4737, 29)]
p = 5 , res = [(491, 23), (1881, 31), (7361, 32)]
p = 6 , res = [(697, 25), (2689, 34), (10561, 35)]
p = 7 , res = [(939, 27), (3641, 36), (14337, 37)]
p = 8 , res = [(1217, 28), (4737, 38), (18689, 40)]
p = 9 , res = [(1531, 29), (5977, 39), (23617, 41)]
The BDDC preconditioner needs more iterations, but the work per iteration is less, so performance is similar to multigrid. This element-wise BDDC preconditioner works well in shared memory parallel as well as in distributed memory mode. Go to \(\S\)2.1.3 for more about BDDC preconditioner.