This page was generated from unit-2.1.1-preconditioners/preconditioner.ipynb.

2.1.1 Preconditioners in NGSolve

Preconditioners are approximate inverses which are used within iterative methods to solve linear or non-linear equations.

Here are some built-in preconditioners in NGSolve:

• Jacobi (local) and block Jacobi

• Direct solvers using sparse factorization (direct)

• Geometric multigrid with different block-smoothers (multigrid)

• Algebraic multigrid preconditioner (h1amg)

• p-version element-level BDDC (bddc)

This tutorial quickly introduces how to use some of these within a solver, and the next two tutorials, 2.1.2 and 2.1.3, continue the preconditioner discussion.

from netgen.csg import unit_cube
from netgen.geom2d import unit_square
from ngsolve import *
import netgen.gui
import matplotlib.pyplot as plt

A simple test problem

In order to experiment with various preconditioners, let us define a simple Poisson solver with the name of a preconditioner as the keyword argument precond.

def SolveProblem(h=0.5, p=1, levels=1,
                 condense = False,
                 precond="local"):
    """
    Solve Poisson problem on l refinement levels.
        h: coarse mesh size
        p: polynomial degree
        l: number of refinement levels
        condense: if true, perform static condensations
        precond: name of a built-in preconditioner
    OUTPUT:
        List of tuples of ndofs and iterations
    """
    mesh = Mesh(unit_square.GenerateMesh(maxh=h))
    # mesh = Mesh(unit_cube.GenerateMesh(maxh=h))
    fes = H1(mesh, order=p, dirichlet="bottom|left")

    u, v = fes.TnT()
    a = BilinearForm(fes, eliminate_internal=condense)
    a += grad(u)*grad(v)*dx
    f = LinearForm(fes)
    f += v*dx
    gfu = GridFunction(fes)
    Draw(gfu)
    c = Preconditioner(a, precond) # Register c to a BEFORE assembly

    steps = []

    for l in range(levels):
        if l > 0:
            mesh.Refine()
        fes.Update()
        gfu.Update()

        with TaskManager():
            a.Assemble()
            f.Assemble()

            # Conjugate gradient solver
            inv = CGSolver(a.mat, c.mat, maxsteps=1000)

            # Solve steps depend on condense
            if condense:
                f.vec.data += a.harmonic_extension_trans * f.vec

            gfu.vec.data = inv * f.vec

            if condense:
                gfu.vec.data += a.harmonic_extension * gfu.vec
                gfu.vec.data += a.inner_solve * f.vec
        steps.append ( (fes.ndof, inv.GetSteps()) )
        if fes.ndof < 15000:
            Redraw()
    return steps

The Preconditioner registers itself to the BilinearForm. Whenever the BilinearForm is re-assembled, the Preconditioner is updated as well.

The local preconditioner

The local preconditioner is a simple Jacobi preconditioner. The number of CG-iterations with the local preconditioner is proportional to \(h^{-1} \sim 2^l\):

SolveProblem(precond="local")

[(8, 4)]

res_local = SolveProblem(levels=9, precond="local")
res_local

[(8, 4),
 (21, 9),
 (65, 25),
 (225, 51),
 (833, 103),
 (3201, 208),
 (12545, 418),
 (49665, 842),
 (197633, 1001)]

Multigrid preconditioner

A geometric multigrid Preconditioner uses the sequence of refined meshes to define a preconditioner yielding optimal iteration numbers (and complexity). It uses a direct solve on the coarsest level, and block Gauss-Seidel smoothers on the refined levels.

res_mg = SolveProblem(levels=9, precond="multigrid")
res_mg

[(8, 2),
 (21, 4),
 (65, 7),
 (225, 8),
 (833, 8),
 (3201, 8),
 (12545, 8),
 (49665, 8),
 (197633, 8)]

plt.xscale("log")
plt.yscale("log")
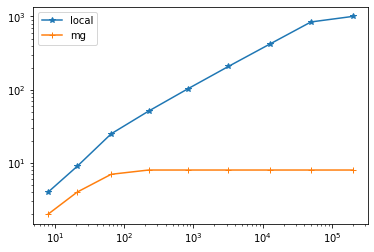
plt.plot(*zip(*res_local), "-*")
plt.plot(*zip(*res_mg), "-+")
plt.legend(['local', 'mg'])
plt.show()

Multigrid implementation for higher order spaces

For high order finite element spaces we use hierarchical bases. Let the (small) sub-spaces \(V_E\), \(V_F\), and \(V_C\) be those generated by basis functions associated with an edge \(E\), a face \(F\), and a cell \(C\), respectively. Then the full space admits the decomposition

\[V_{hp} = V_{p=1} + \sum_{\text{edges }E} V_E + \sum_{\text{faces }F} V_F + \sum_{\text{cells }C} V_C\]

where \(V_{p=1}\) refers to the lowest order finite element subspace. The system matrix then takes the block form

\[\begin{split}A = \left( \begin{array}{cccc} A_{VV} & A_{VE} & A_{VF} & A_{VC} \\ A_{EV} & A_{EE} & A_{EF} & A_{EC} \\ A_{FV} & A_{FE} & A_{FF} & A_{FC} \\ A_{CV} & A_{CE} & A_{CF} & A_{CC} \\ \end{array} \right)\end{split}\]

where the \(A_{VV}\)-block is exactly the system matrix of a lowest order method, representing the part of operator acting on the \(V_{p=1}\) subspace.

NGSolve’s multigrid implementation for a high order method uses h-version multigrid for the lowest order block, and local block-smoothing for the high order bubble basis functions.

for p in range(1,10):
    r = SolveProblem(h=0.5, p=p, levels=4, condense=False,
                     precond="multigrid")
    print ("p=", p, ": ndof,nsteps=", r)

p= 1 : ndof,nsteps= [(8, 2), (21, 4), (65, 7), (225, 8)]
p= 2 : ndof,nsteps= [(21, 5), (65, 6), (225, 8), (833, 8)]
p= 3 : ndof,nsteps= [(40, 9), (133, 12), (481, 12), (1825, 13)]
p= 4 : ndof,nsteps= [(65, 12), (225, 15), (833, 16), (3201, 16)]
p= 5 : ndof,nsteps= [(96, 14), (341, 19), (1281, 20), (4961, 20)]
p= 6 : ndof,nsteps= [(133, 16), (481, 23), (1825, 23), (7105, 23)]
p= 7 : ndof,nsteps= [(176, 18), (645, 25), (2465, 26), (9633, 26)]
p= 8 : ndof,nsteps= [(225, 19), (833, 27), (3201, 28), (12545, 28)]
p= 9 : ndof,nsteps= [(280, 20), (1045, 29), (4033, 30), (15841, 30)]

We observe that the number of iterations grows mildly with the order, and remains bounded with mesh refinement.

Performing static condensation improves the situation:

for p in range(1,10):
    r = SolveProblem(h=0.5, p=p, levels=4, condense=True,
                     precond="multigrid")
    print ("p=", p, ": ndof,nsteps=", r)

p= 1 : ndof,nsteps= [(8, 2), (21, 4), (65, 7), (225, 8)]
p= 2 : ndof,nsteps= [(21, 5), (65, 6), (225, 8), (833, 8)]
p= 3 : ndof,nsteps= [(40, 5), (133, 6), (481, 7), (1825, 8)]
p= 4 : ndof,nsteps= [(65, 5), (225, 6), (833, 7), (3201, 8)]
p= 5 : ndof,nsteps= [(96, 5), (341, 6), (1281, 7), (4961, 8)]
p= 6 : ndof,nsteps= [(133, 5), (481, 6), (1825, 7), (7105, 8)]
p= 7 : ndof,nsteps= [(176, 5), (645, 6), (2465, 7), (9633, 8)]
p= 8 : ndof,nsteps= [(225, 5), (833, 6), (3201, 7), (12545, 8)]
p= 9 : ndof,nsteps= [(280, 5), (1045, 6), (4033, 7), (15841, 8)]

Element-wise BDDC preconditioner

A built-in element-wise BDDC (Balancing Domain Decomposition preconditioner with Constraints) preconditioner is also available. In contrast to local or multigrid preconditioners, the BDDC preconditioner needs access to the element matrices. This is exactly the reason why we register the preconditioner with the bilinear form bfa before calling bfa.Assemble().

for p in range(1,10):
    r = SolveProblem(h=0.5, p=p, levels=4, condense=True,
                     precond="bddc")
    print ("p=", p, ": ndof,nsteps=", r)

p= 1 : ndof,nsteps= [(8, 2), (21, 2), (65, 2), (225, 2)]
p= 2 : ndof,nsteps= [(21, 7), (65, 12), (225, 16), (833, 17)]
p= 3 : ndof,nsteps= [(40, 11), (133, 16), (481, 20), (1825, 22)]
p= 4 : ndof,nsteps= [(65, 13), (225, 18), (833, 24), (3201, 26)]
p= 5 : ndof,nsteps= [(96, 14), (341, 19), (1281, 26), (4961, 29)]
p= 6 : ndof,nsteps= [(133, 14), (481, 20), (1825, 28), (7105, 31)]
p= 7 : ndof,nsteps= [(176, 15), (645, 22), (2465, 30), (9633, 33)]
p= 8 : ndof,nsteps= [(225, 16), (833, 23), (3201, 31), (12545, 35)]
p= 9 : ndof,nsteps= [(280, 16), (1045, 24), (4033, 33), (15841, 36)]

The BDDC preconditioner needs more iterations, but the work per iteration is less, so performance is similar to multigrid. This element-wise BDDC preconditioner works well in shared memory parallel as well as in distributed memory mode. See \(\S\)2.1.3 for more about BDDC preconditioner and how to combine it with an algebraic multigrid coarse solver.